广度优先搜索
广度优先搜索通常用来找到两个节点间的最短路径。然后还可以扩展到:下棋时,走多少步可以获胜;找到人际关系中最近的医生等。
该算法用的数据结构是图。
图,由节点和边组成。一个节点可能和多个节点相连,这些节点被称为邻居。
比如我们常见的场景:我们人大双子峰,想前往金门大桥,要看最短的路线。这个我们平常出行经常用到的地图APP里会有提供。比如位置信息如下:
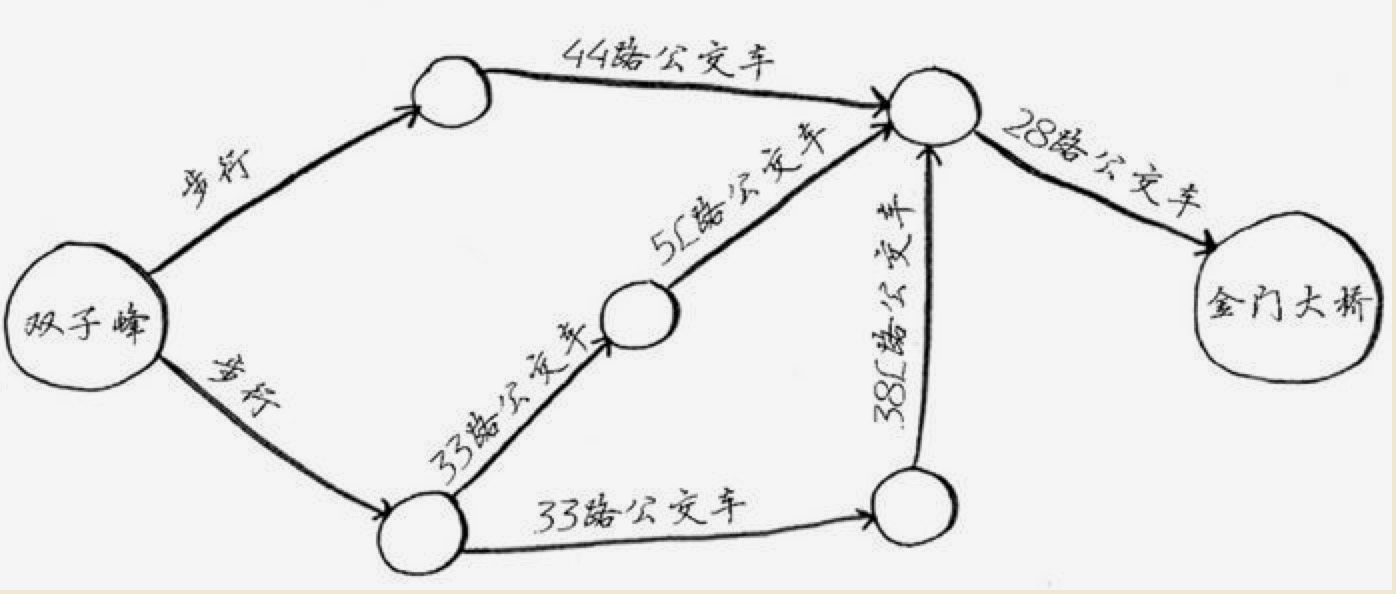
要算出线路。我们可以先考虑:从起点开始,一步就能到终点吗?和起点相邻的节点并不包括终点;那么,两步呢?这时候就要看和起点相邻的几个节点各自的相邻节点里是否包括终点,如果还不包括,继续检查直到找到终点。
这样一层一层的去查找,就可以找到终点的最少步数。除了一层一层的找,还可以按深度优先的方式。具体方法是先查找他的一个邻节点,如果不是终点,再查该节点的邻节点,这样一直追下去。
为了体现搜索时的顺序,这里要用到“队列”,它是一种先进先出的数据结构。也就是说先添加进队列的节点要先进行比较。和它对应的是“栈”,它是先进后出,可以被用来作字符串匹配,计算公式。计算机运算程序时,用的栈。
案例:你的人际关系中有芒果销售商吗?
假设你的朋友关系网如下:
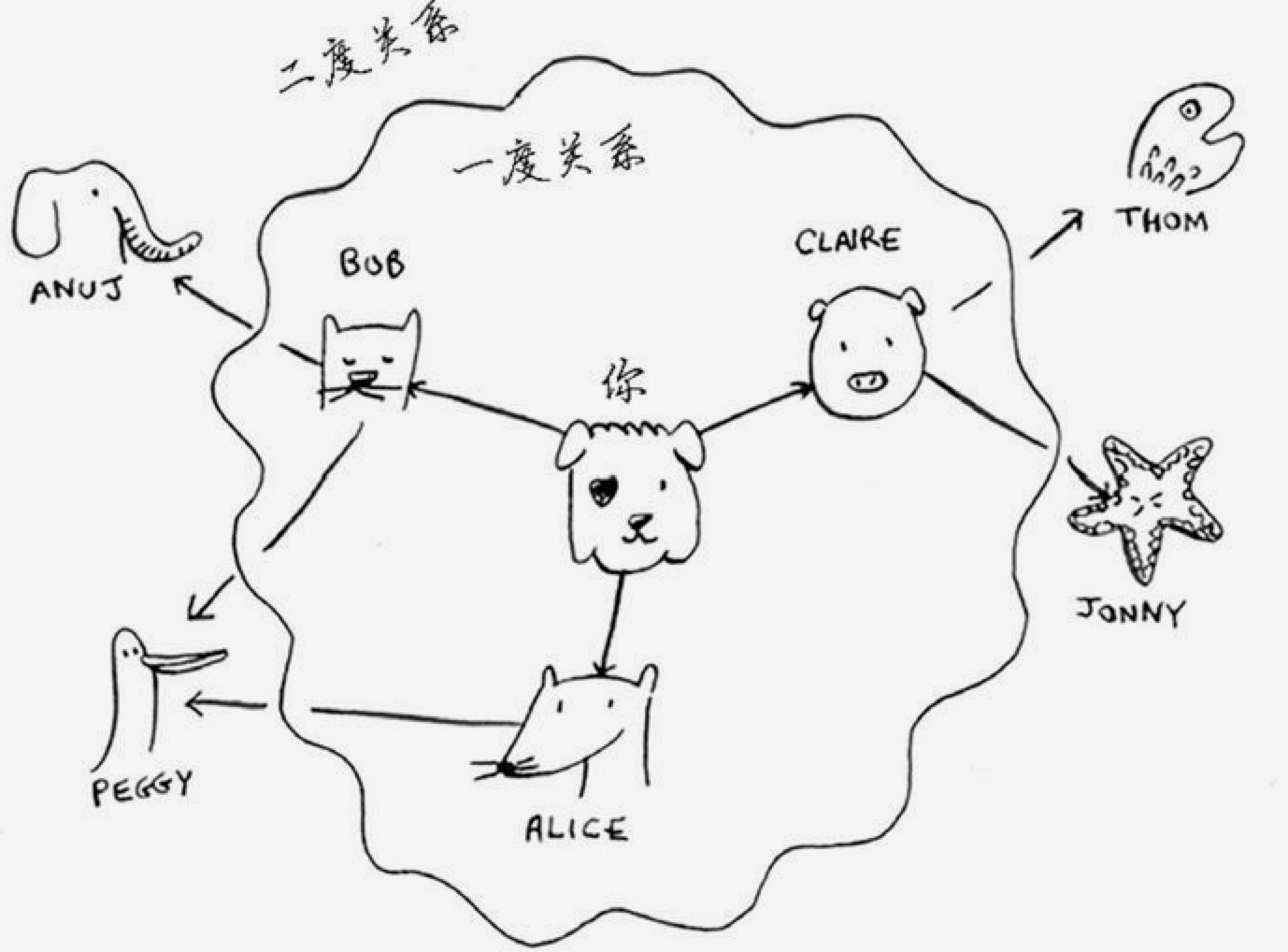
你的朋友就是和你相邻的节点。这一圈关系可以被称为一度关系;而他们的朋友被称为二度关系;依此类推。
要找到目标,我们可以这样做:
- 先将我的一度关系加到队列中。然后在其实进行搜索目标。如果有目标,直接找到。
- 如果一度关系队列中没有,将各个一度关系人对应的邻节点(也就是我的二度关系)加到队列,然后比较。
如果队列比较完了还没找到目标,说明人际关系中没有芒果销售商。比较过程可能如下:
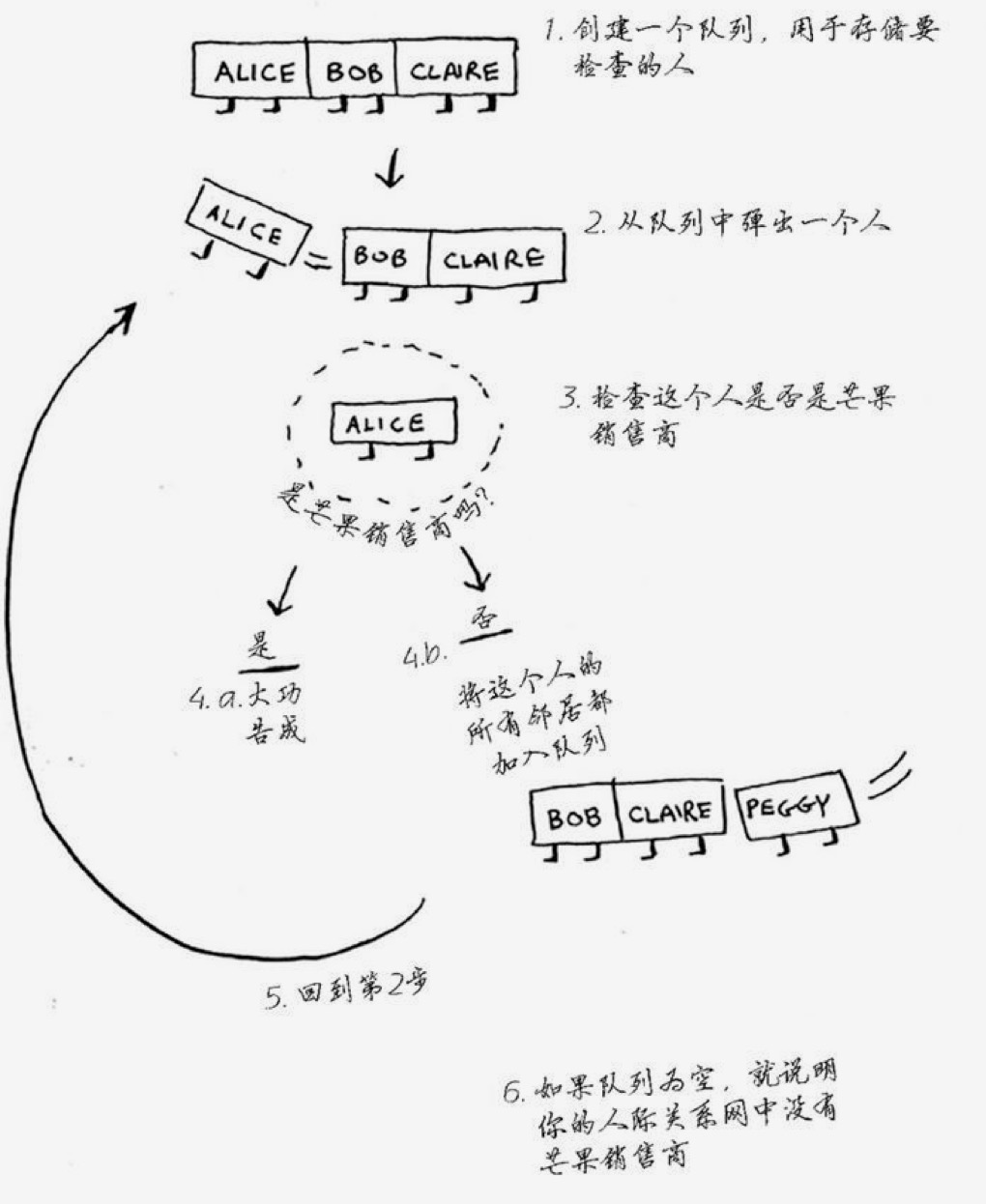
在实际应用中,我们要注意的是要去重。因为不同的人可能有同一个好友。这样可能会造成死循环,不停的把已经判断过的人加到队列中。所以对于已经判断过的人,要做标记,后面不再判断。
简单的PHP代码可能如下:
$realation = array();
$realation['you'] = array('alice', 'bob', 'claire');
$realation['alice'] = array('peggy');
$realation['bob'] = array('anuj', 'peggy');
$realation['claire'] = array('thom', 'jonny');
$realation['anuj'] = array();
$realation['peggy'] = array('you');
$realation['thom'] = array();
$realation['jonny'] = array();
$checkedList = array();
$search_queue = array();
function isSeller($name){
if($name == 'jonny'){
return true;
}
return false;
}
$search_queue = array_merge($search_queue, $realation['you']);
while(count($search_queue) > 0){
$person = array_shift($search_queue);
print_r("Check $person" . PHP_EOL);
if(array_key_exists($person, $checkedList)){
print_r("$person has checked! ignore!" . PHP_EOL);
continue;
}
if(isSeller($person)){
print_r("$person is a seller!" . PHP_EOL);
break;
}else{
// 不是销售商,将他的朋友添加到队列
print_r("$person is not a seller, add his friend to queue!" . PHP_EOL);
$checkedList[$person] = 1;
$search_queue = array_merge($search_queue, $realation[$person]);
}
}
迪杰斯特拉
通过广度优先算法,我们可以找到达到目的的最短路径或者最小步数。但步数最小不一定是最优的路径。比如我们使用地图APP时,从A到B,通常会有:时间最短、路最短等多条路径可以选择。因为有的路段虽然距离上是最短的但可能堵车,这样时间就长了。
比如从双子峰到金门大桥,用广度优先算法找到的路径可能是:
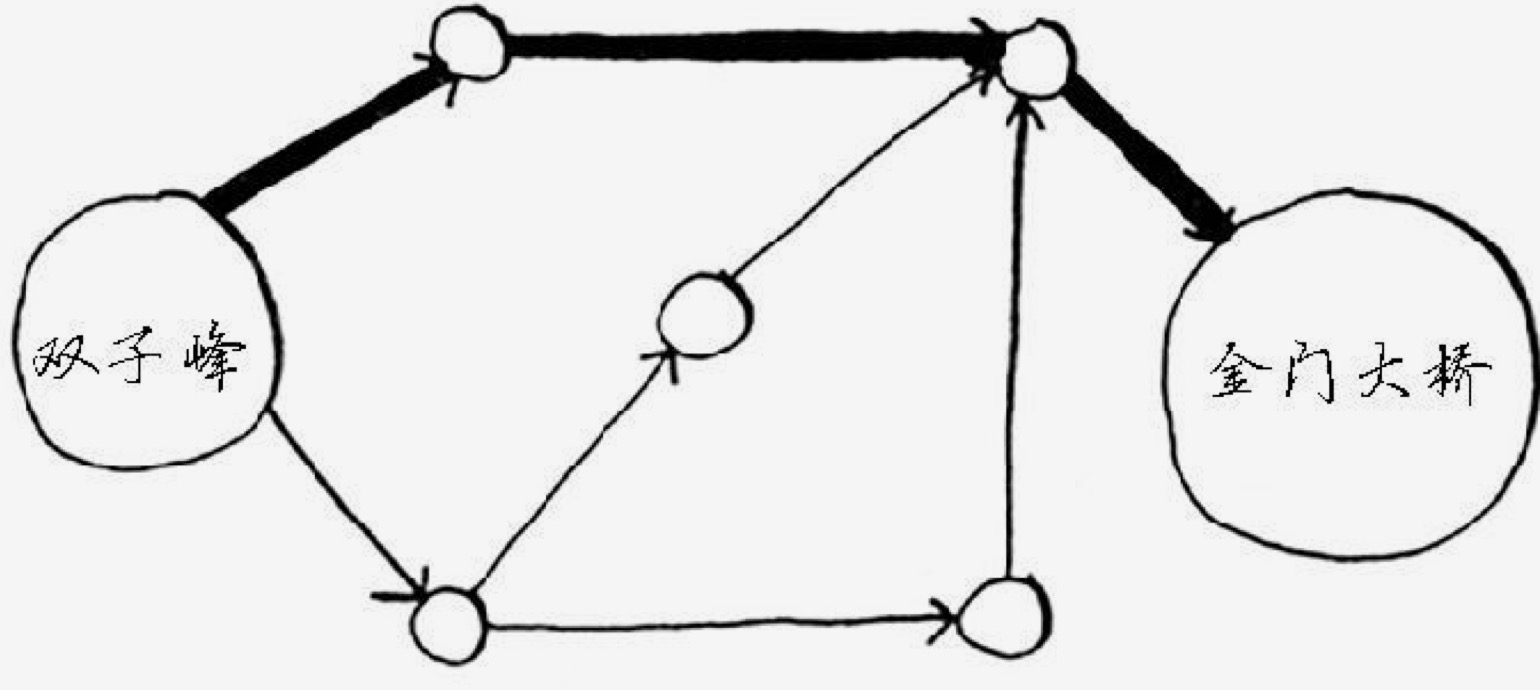
但如果每段路的时间如下,则最优路线可能是这样的:
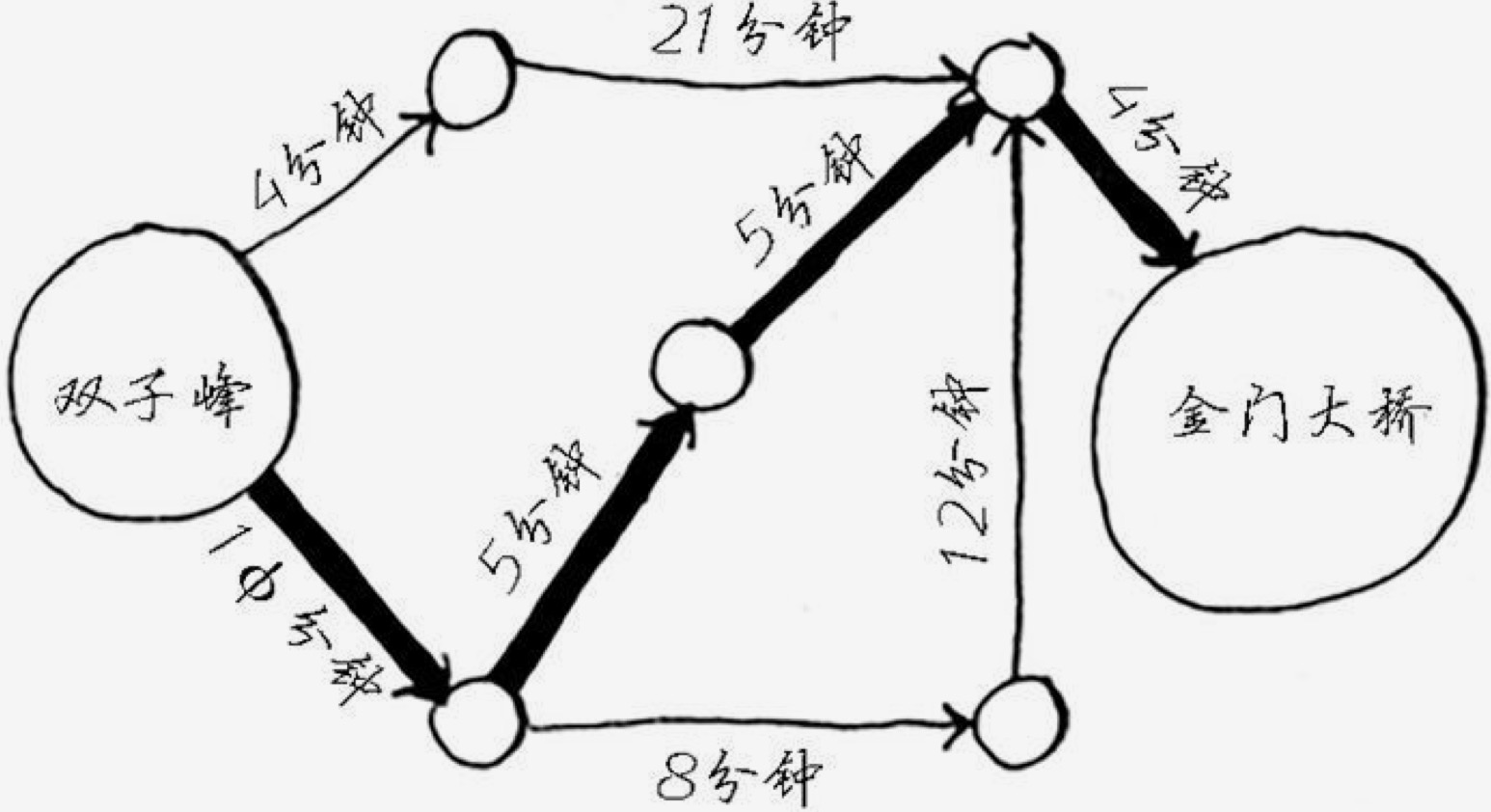
迪杰斯特拉算法的目标是找到从起点到各个节点最少的成本。因为每条路线上都会有相应的成本,比如从A到B可能是时间的成本、可能是距离的成本。主要是为了应对一个目标有多种方案的时候。
举例
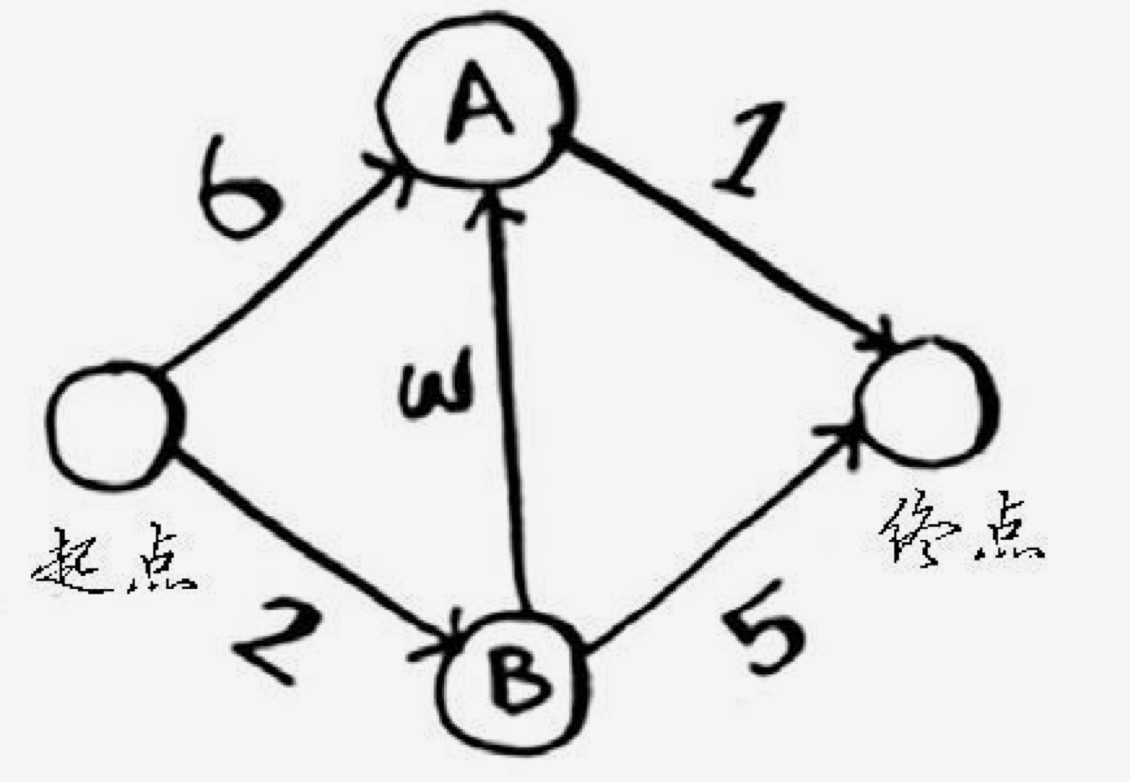
- 找到从起点到各相邻节点的成本。到A是 6,到B是2。到终点是我们要计算的值,目前是未知。
我们可以维护一个成本表,如下:
节点 成本 A 6 B 2 终点 未知 - 从成本表中选择当前成本最低的点,从它开始,再计算到它的相邻点的成本。它到A是 3,到终点是 5。这时候可以更新成本表。因为发现到A的成本可以变为先到B,然后再到A,和是 5,比之前的 6 要小。而且可以通过B直接到终点了。这时候成本表是:
节点 成本 A 2+3=5 B 2 终点 2+5=7 - 继续选择成本最低的,未处理过的节点,这时是从A开始算,会发现从A到终点成本要更低。这时候成本表如下:
节点 成本 A 5 B 2 终点 5+1=6
这样,所有的节点路线都算完了,得到最小的到终点的成本是 6。这就是最优路线了。要注意的是,对于已经处理过的节点,我们就不再处理了。
但我们从成本表里无法知道是怎么到的终点,所以我们可以在成本表里添加一些信息,表示是从哪些节点到的终点。
实例: 物品交换
Rama 有一本乐谱,Alex 有一个海报,并且愿意等价交换乐谱;另外还有许多其它的物品可以用来交换,不过交换的时候可能需要加钱。它们的交换关系如下:
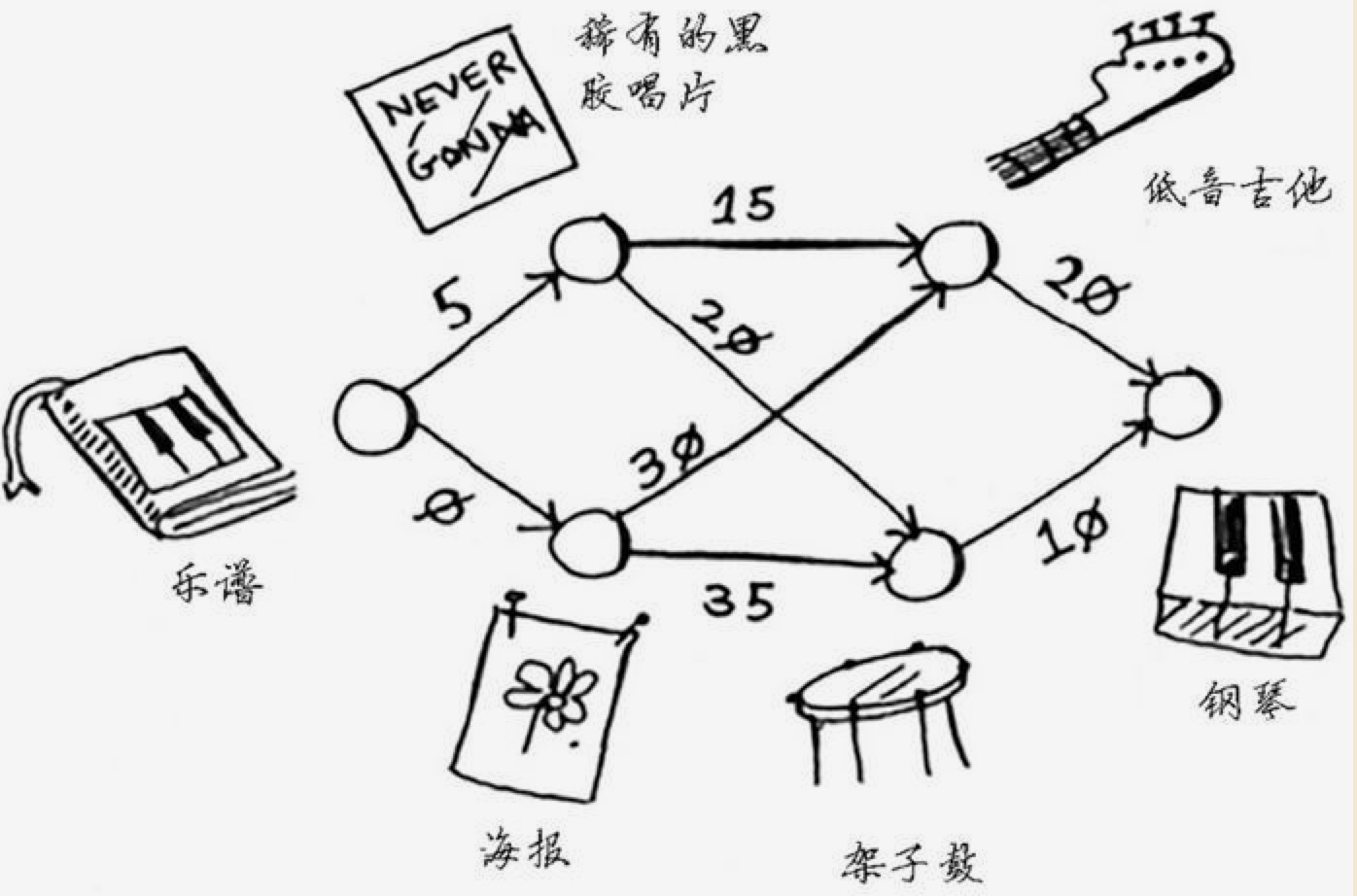
目标是要找到用乐谱交换钢琴的最少成本交换方式。
现在开始用上面的步骤一步步处理:
- 从乐谱开始,计算它到相邻节点的成本。并加到成本表。这时的成本表如下:
父节点 物品 成本 乐谱 唱片 5 乐谱 海报 0 -- 钢琴 未知 - 从目前的成本表中找到最小成本的节点:海报,然后把他的相邻节点进行计算。这时的成本表是:
父节点 物品 成本 乐谱 唱片 5 乐谱 海报 0 海报 吉他 30 海报 架子鼓 35 -- 钢琴 未知 - 目前 成本表中最低的低是唱片,计算它对应的相邻节点。这时候会发现到吉他和架子鼓这个节点的成本要比目前成本表中的要低,所以需要更新成本表:
父节点 物品 成本 乐谱 唱片 5 乐谱 海报 0 唱片 吉他 20 唱片 架子鼓 25 -- 钢琴 未知 要注意这里,吉他和架子鼓的父节点从上一步的海报变成了唱片。
- 这时候要处理成本表中下一个最低成本的节点:吉他。要更新它节点的成本。成本表如下:
父节点 物品 成本 乐谱 唱片 5 乐谱 海报 0 唱片 吉他 20 唱片 架子鼓 25 吉他 钢琴 40 - 最后一个没处理的节点:架子鼓,我们对它进行处理。发现了到钢琴更低的成本。成本表:
父节点 物品 成本 乐谱 唱片 5 乐谱 海报 0 唱片 吉他 20 唱片 架子鼓 25 架子鼓 钢琴 35 - 所有节点都处理完毕。这时候成本表中到钢琴的成本就是最低的成本了。而且根据父节点,我们可以完整的知道交换的路径:乐谱–>唱片–>架子鼓–>钢琴
负成本的情况
如果有时候出现一个路径成本为负,这时候就要注意了。或者绕一大圈后再回来的情况。如:
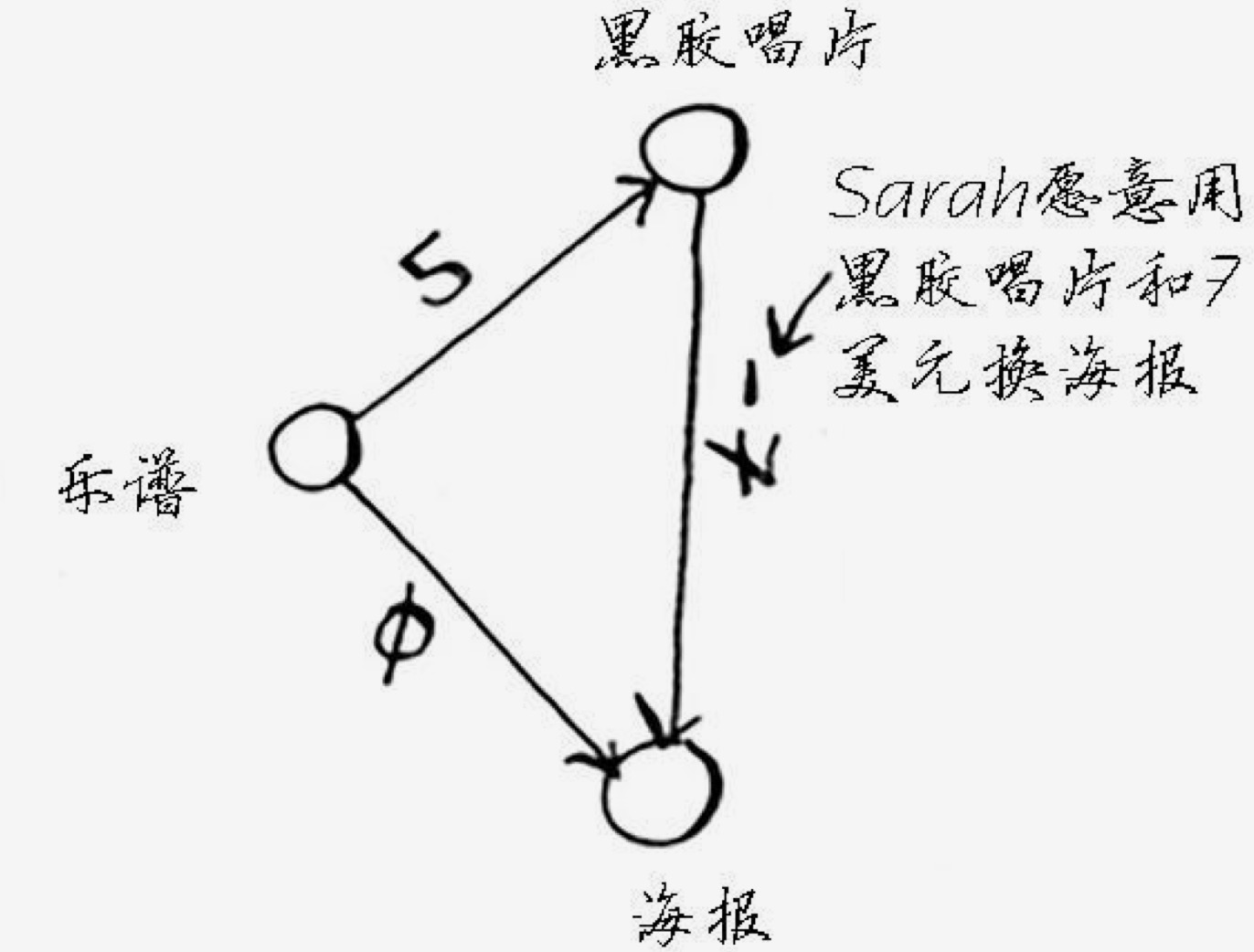
可以看到唱片换海报会倒贴 7 块钱。通过观察我们可以看到会有两种方式交换到架子鼓,最优的方式是 33 块钱的成本。
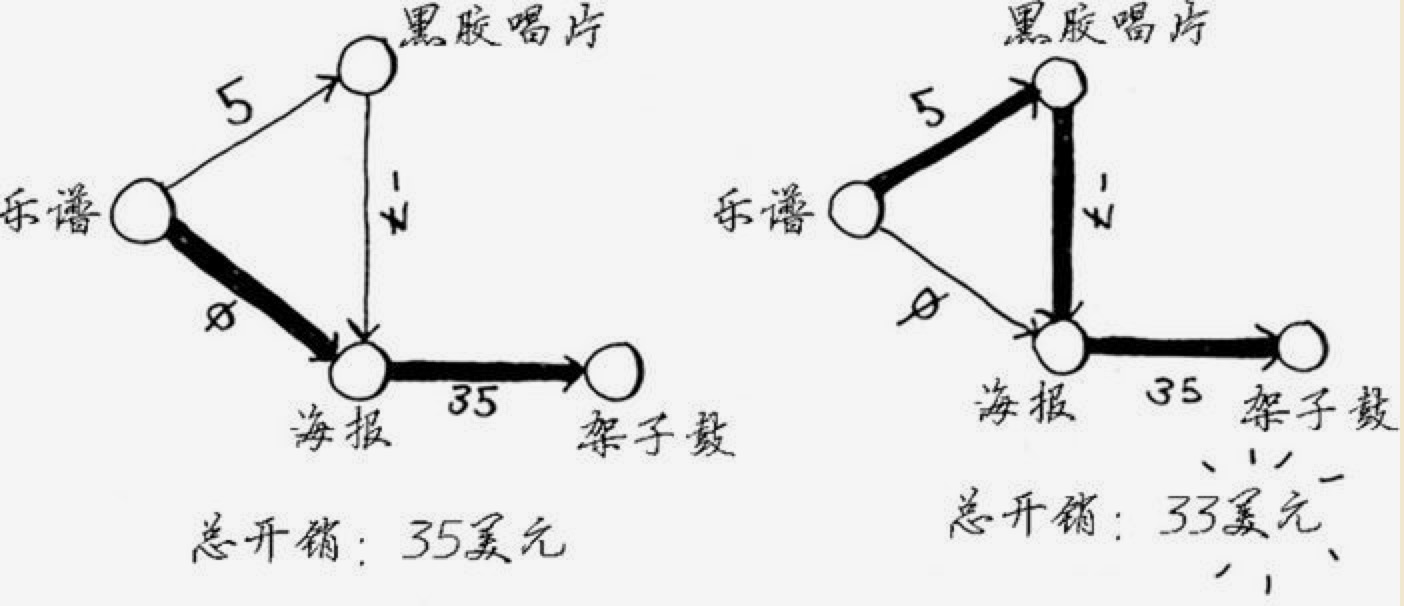
我们一步步拆解从乐谱到架子鼓的过程。
- 处理乐谱。这时候的成本表是:
父节点 物品 成本 乐谱 唱片 5 乐谱 海报 0 -- 钢琴 未知 - 处理成本表中最低成本的节点:海报。这时候成本表:
父节点 物品 成本 乐谱 唱片 5 乐谱 海报 0 海报 架子鼓 35 - 处理成本表中最低成本的点:唱片。对于海报,上一步已经处理过了,后面不会再处理了。这就是问题的关键。这一步会发现到海报有更低的成本。但海报的领节点我们都已经计算成本并添加到成本表了。如果现在要更新到海报的成本,那么海报相邻节点的成本全部都要重新计算。按迪杰斯特拉的逻辑,现在的成本表是:
父节点 物品 成本 乐谱 唱片 5 乐谱 海报 -2 海报 架子鼓 35
目前成本表中,已经没有未处理的节点了,架子鼓没有相邻节点,所以算法退出了。这时候算法得到的成本是 35 元。但实际上我们知道是有一种 33 元的方案。
之所有算法没有找到 33 元的方案就是因为我们更新海报的值为 -2 的时候,并没有把海报的相邻节点重新计算一遍。如果这样干,那就叫Bellman-Ford算法,不是迪杰斯特拉了。
代码示例
要计算起点到终点最低成本:
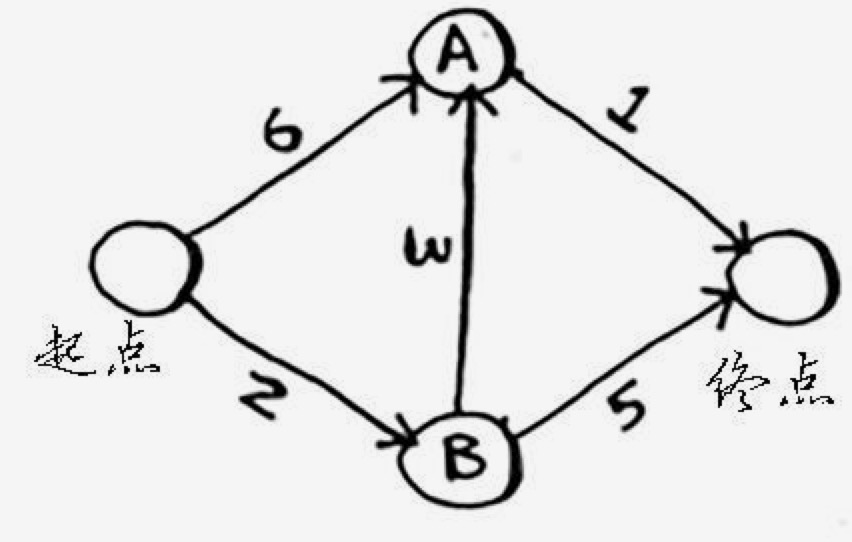
代码如下:
// 构建整体数据
$data = array();
$data['start']['a'] = 6;
$data['start']['b'] = 2;
$data['a']['final'] = 1;
$data['b']['a'] = 3;
$data['b']['final'] = 5;
$data['final'] = array();
// 构建成本数据并初始化初始节点
$costs = array();
$costs['start']['value'] = 0;
$costs['start']['parent'] = null;
function findLowestNode($costs){
if(!is_array($costs) || count($costs) < 1){
return null;
}
$lowEstKey = null;
$lowEstVal = null;
foreach ($costs as $key => $loop) {
// 已经处理过的节点不再处理
if(array_key_exists('deal', $loop)){
continue;
}
// 终点节点不处理
if($key == 'final'){
continue;
}
// 找出最小值节点
$val = $loop['value'];
if($lowEstKey === null){
$lowEstKey = $key;
$lowEstVal = $val;
}
if($val < $lowEstVal){
$lowEstKey = $key;
$lowEstVal = $val;
}
}
if($lowEstKey === null){
return null;
}
return array($lowEstKey, $lowEstVal);
}
$nowLowest = findLowestNode($costs);
while ($nowLowest != null){
list($nowLowestKey, $nowLowestVal) = $nowLowest;
$neighbors = $data[$nowLowestKey];
foreach ($neighbors as $key => $loop) {
$newCost = $nowLowestVal + $loop;
// 如果成本表中还没有该相邻节点,把当前节点加入到成本表
if(!array_key_exists($key, $costs)){
$costs[$key]['value'] = $newCost;
$costs[$key]['parent'] = $nowLowestKey;
}else{
// 如果有更优方案.更新当前节点的父节点和成本
if($newCost < $costs[$key]['value'] || $costs[$key]['value'] == null){
$costs[$key]['value'] = $newCost;
$costs[$key]['parent'] = $nowLowestKey;
}
}
}
// 标记为已处理
$costs[$nowLowestKey]['deal'] = 1;
// 再获得当前成本表中最低成本的节点
$nowLowest = findLowestNode($costs);
}
$road = array();
$node = $costs['final'];
while($node['parent'] != 'start'){
array_push($road, $node['parent']);
$node = $costs[$node['parent']];
}
$road = array_reverse($road);
array_unshift($road, 'start');
array_push($road, 'final');
print_r($road);
如果跟踪打印 $cost 的值可以发现算法先找出了成本为 7 (起点->b->终点)的方案,然后又找到了更优的方案(起点->b->终点),成本为 6。
扩展
有了上面的程序,我们就可以浪起来了,只把图的数据改一下,程序主体逻辑不变,就可处理其它任何的情况了。看一下下面几种情况:
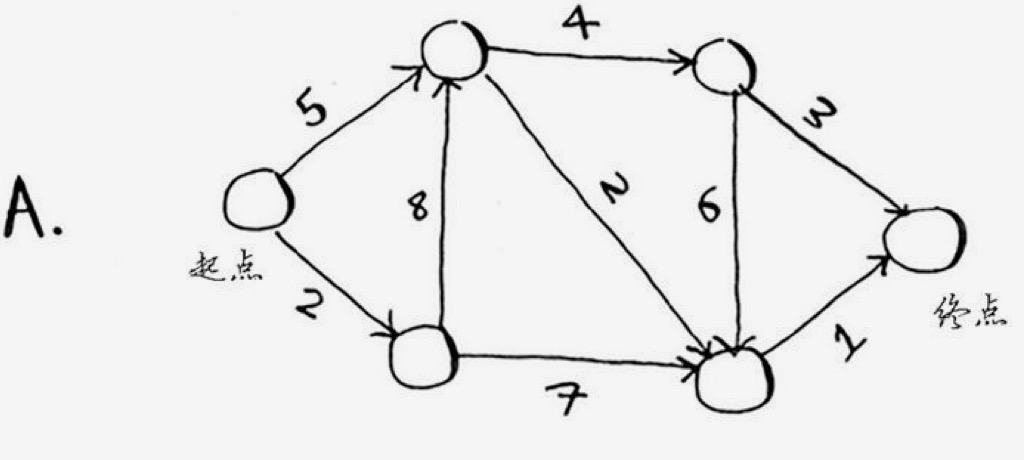
// 构建整体数据
$data = array();
$data['start']['a'] = 5;
$data['start']['b'] = 2;
$data['a']['c'] = 4;
$data['a']['d'] = 2;
$data['b']['d'] = 7;
$data['b']['a'] = 8;
$data['c']['final'] = 3;
$data['c']['d'] = 6;
$data['d']['final'] = 1;
$data['final'] = array();
// 运算结果是 8
// start->a->d->final
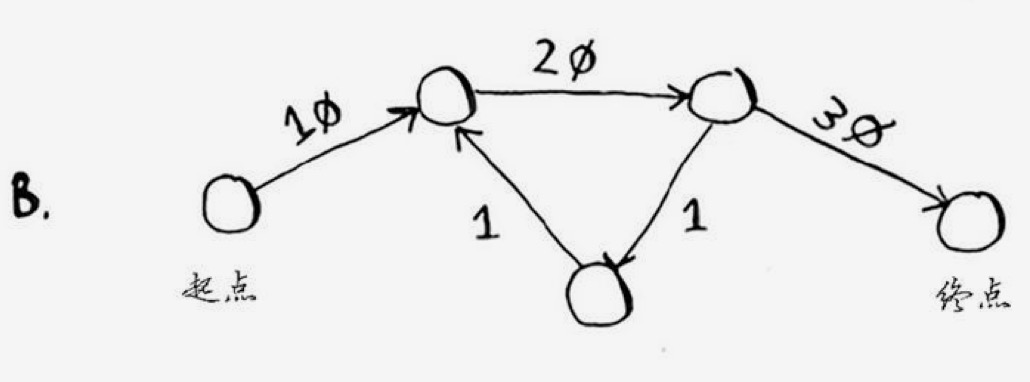
// 构建整体数据
$data = array();
$data['start']['a'] = 10;
$data['a']['b'] = 20;
$data['b']['final'] = 30;
$data['b']['c'] = 1;
$data['c']['a'] = 1;
$data['final'] = array();
//运行结果是 60
// start->a->b->final
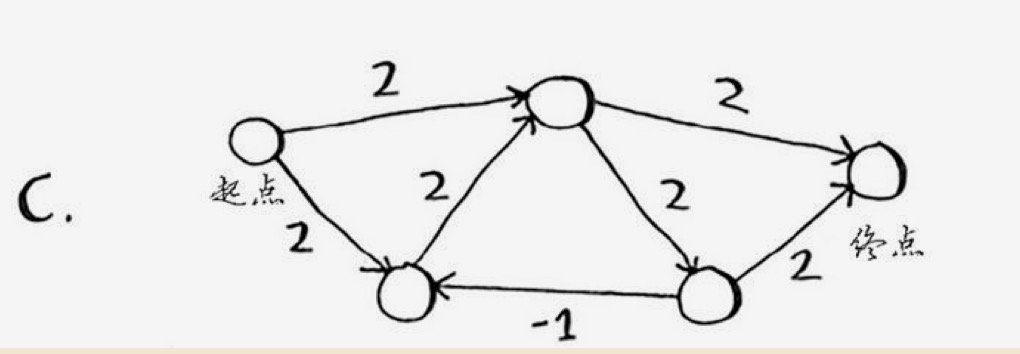
// 构建整体数据
$data = array();
$data['start']['a'] = 2;
$data['start']['b'] = 2;
$data['a']['c'] = 2;
$data['a']['final'] = 2;
$data['b']['a'] = 2;
$data['c']['b'] = -1;
$data['c']['final'] = 2;
$data['final'] = array();
// 运行结果是 4.但存在负边.要注意.结果可能不准
// start->a->final