最小二乘法

又称最小平方法，是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

示例

四个数据点: (1, 6)、（2， 5）、（3， 7）、（4， 10）。我们希望找到一条直线，和这几个点最匹配。即：

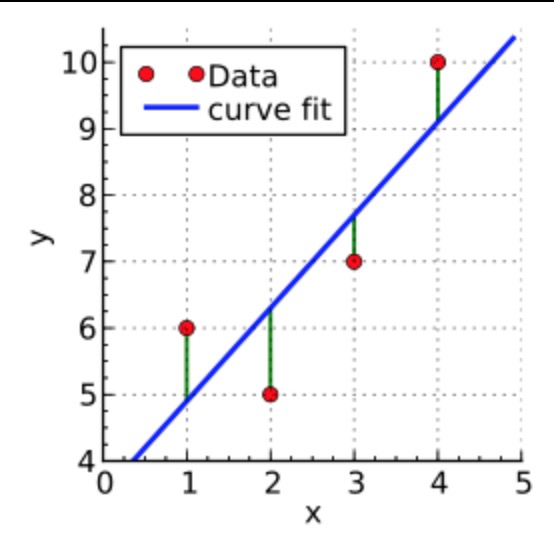
我们假设该直线的表达式是：y = α₁ + α₂x。那么，按现有数据来看就有：

α₁ + 1α₂ = 6

α₁ + 2α₂ = 5

α₁ + 3α₂ = 7

α₁ + 4α₂ = 10

该线上点对应的值和真实值是有误差的，我们要做的是找到相应的 α 值，让误差最小。最小二乘法采用的手段是使误差的平方的和最小，即：

S(α₁, α₂) = [6 - (α₁ + 1α₂)]² + [5 - (α₁ + 2α₂)]² + [7 - (α₁ + 3α₂)]² + [10 - (α₁ + 4α₂)]²

要求 S 的最小值。而求它最小值又可以通过求 α₁, α₂的偏导数，并让结果等于 0 得到。即:

∂S/∂α₁ = 0 = 8α₁ + 20α₂ - 56

∂S/∂α₂ = 0 = 20α₁ + 60α₂ - 154

可以解出 α₁ = 3.5, α₂ = 1.4，也就是说直线的函数是:

y = 3.5 + 1.4x

推导

对由某一变量 t 或多个变量 t₁ …… t_n 构成的相关变量 y。