欢迎来到夜宇工作间
这里是我的个人IT学习回忆录-
回归
回归常用于数据挖掘,疾病自动诊断,经济预测等领域。例如,探讨引发疾病的危险因素,并根据危险因素预测疾病发生的概率等。
回归的目的是用来预测数值型的目标值。最直接的办法是写一个公式依据输入数据得到结果。比如,想要预测姐姐男友汽车功率的大小,可能的公式是:
功率 = 0.0015 * 每月薪水 + 0.99 * 存款数额
这个计算公式就是回归方程,而公式中的 0.0015, 0.99 就是回归系数。这里的薪水,存款,叫做因数变量,而功率叫做自变量。
通过许多测试数据及结果反向推算出系数值的过程就叫回归。意思就是:目前已经有了许多完整的数据,包括了 N 个人的汽车功率大小以及他们的每月薪水及存款数额,但我们不知道回归系数分别取多少才是合适的,我们需要计算出来,找到一个对所有测试数据都合适的值。
当然,我们得到系数后,再把每个人的数据代入公式,计算理到的最终值与每个人的实际值之间肯定会有误差。
回归分析是被用来研究一个结果变量(自变量)与一个或多个原因变量(因变量)之间关系的统计技术。以胃癌病情分析为例,选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群必定具有不同的体征与生活方式等。因此因变量就为是否胃癌,值为“是”或“否”,自变量就可以包括很多了,如年龄、性别、饮食习惯、幽门螺杆菌感染等。通过回归分析,可以得到自变量的权重,从而可以大致了解到底哪些因素是胃癌的危险因素。同时根据该权重可以根据危险因素预测一个人患癌症的可能性。
我们要做的就是找出各个因变量的权重,即回归系数。
象这种,认为自变量的值是各个因变量乘以回归系数再相加的方式叫作 线性回归。也有不认为它们是相加的,认为它们是相乘或相除的。
线性回归
我们假设自变量 y 与因变量 x1,x2,⋯,xn之间具有线性相关的关系,那么用公式就可以将线性回归模型表示为:
y = f(xi)=w1x1+⋯+wnxn
可以看出就是一个矩阵相乘的算法。
简化为: y = wTx
w 就是回归系数。
如果只有一个因变量,将因变量的值做为横坐标,自变量做为纵坐标。 这就相当于,我们知道了一些数据点,要找一条合适的线,让他们最大程度的拟合。这就是线性回归。即:
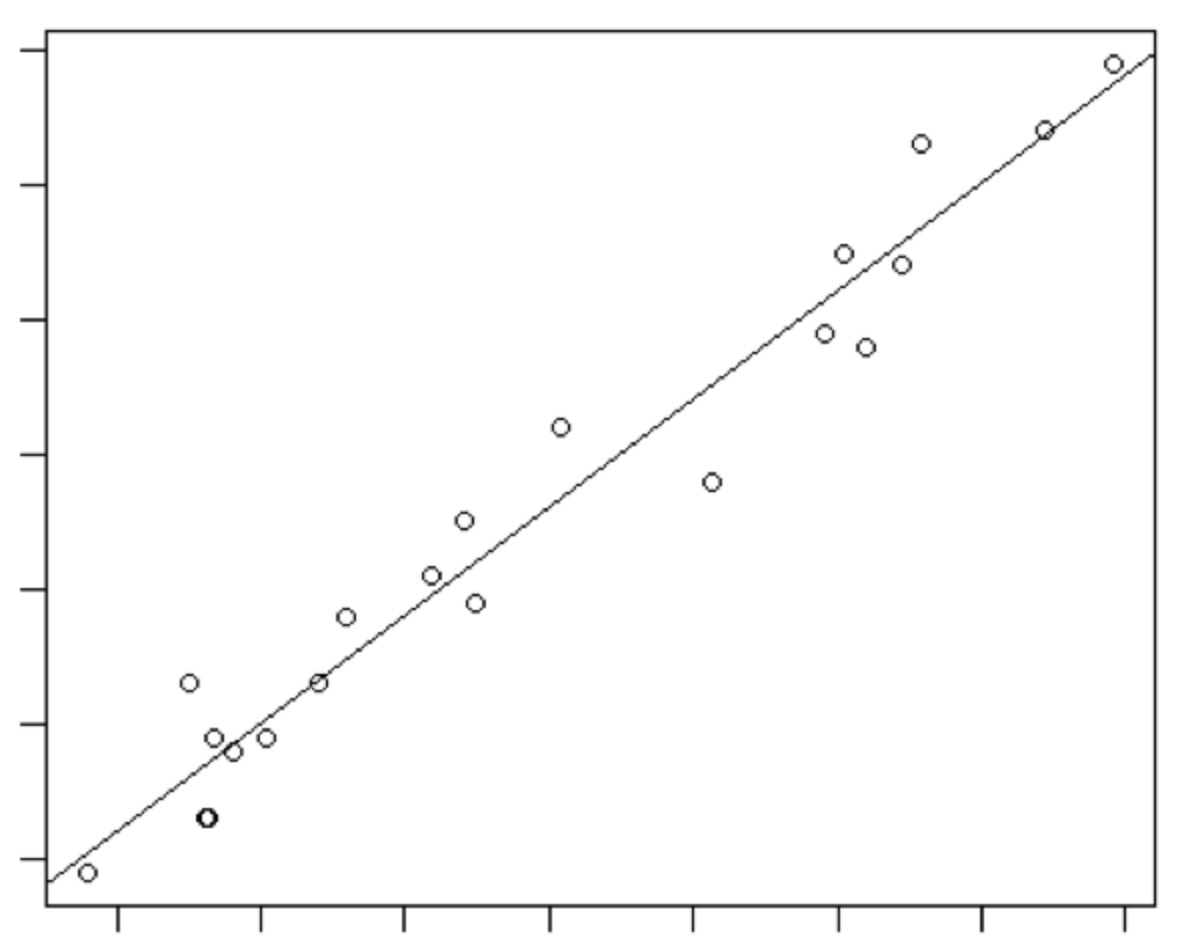
如果因变量有多个。用图表示:
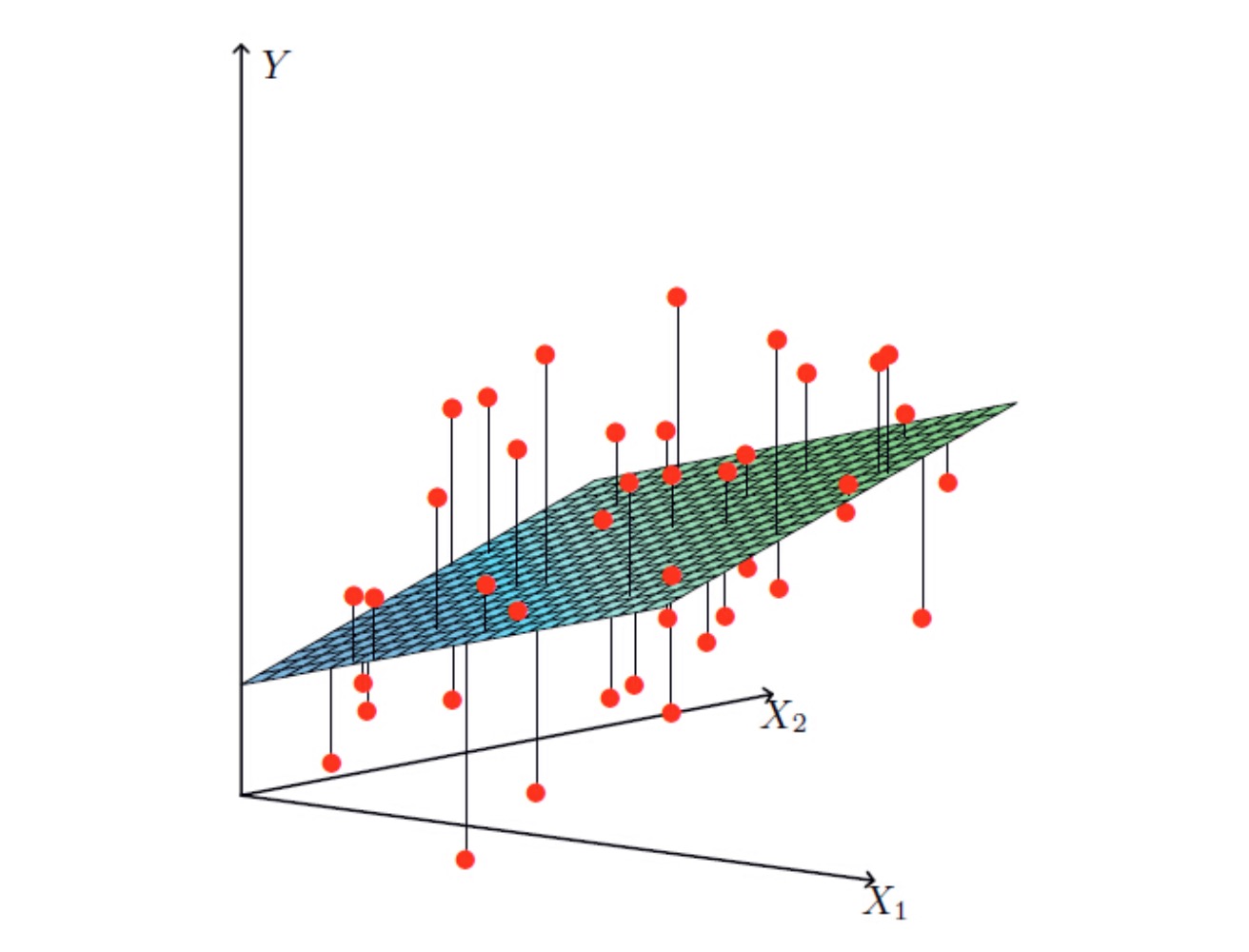
已经有一堆数据 x 了,如何从中推导出回归系数 w 呢?一个常用的方法是找出使误差最小的 w。这里的误差指的就是公式计算出来的预测值 wTx 和真实值 y 之间的差值。我们要计算所有测试样本的误差(wTx - y),然后取一个最适中的值。由于误差可能为正,也可能为负,为了得到最合适的值,我们把所有的误差取平方然后相加。即:最小二乘法(最小平方法)。
所以,误差的平方差表示为: ∑(yi - wxiT)2
在矩阵的世界中,矩阵的平方可以表示为矩阵乘以矩阵的转置。
所以,差值用矩阵来表示,则是:(y-wX)T(y-wX) 对它求导数得到:XT(y-wX)。这就是误差值的表达式,在最理想的情况下,误差值是 0。
0 = XT(y-wX)
0 = XTy - wXTX
w = XT / XTX
而除法的意思是取逆,所以 w 的值:
w = XT(XTX)-1y
其中:XTX 表示 X 转置后再和 X 相乘,(XTX)-1 表示再将相乘的结果取逆。
案例:求回归系数
现有如下测试数据:
1.000000 0.067732 3.176513 1.000000 0.427810 3.816464 1.000000 0.995731 4.550095 1.000000 0.738336 4.256571 1.000000 0.981083 4.560815 1.000000 0.526171 3.929515 1.000000 0.378887 3.526170 1.000000 0.033859 3.156393 1.000000 0.132791 3.110301测试的代码:
# 读取测试数据,返回因变量和自变量矩阵两个列表 def loadDataSet(fileName): numFeat = len(open(fileName).readline().split('\t')) - 1 dataMat = []; labelMat = [] fr = open(fileName) for line in fr.readlines(): lineArr =[] curLine = line.strip().split('\t') for i in range(numFeat): lineArr.append(float(curLine[i])) dataMat.append(lineArr) labelMat.append(float(curLine[-1])) return dataMat,labelMat # 标准的线性回归 def standRegres(xArr, yArr): xMat = mat(xArr) yMat = mat(yArr).T xTx = xMat.T * xMat if linalg.det(xTx) == 0.0: print "该矩阵是奇异的,不能取逆" return ws = xTx.I * (xMat.T*yMat) return ws # 加载测试数据 xar, yar = loadDataSet("ex0.txt") # 用线性回归计算回归系数 # 得到的结果是一个行向量 res = standRegres(xar, yar) # 通过回归系数,为一个新数据推测结果值 # 声明一个测试数据数组,然后转换为矩阵,转换完后,它是一个列向量 test_data = mat([1, 0.378887]) # 由于 test_data 是一个列向量,res 是行向量,所以两者就没必要进行转置了。可以直接相乘 # 就算拿我们测试数据中现有的值来计算,它的结果和原来的结果也会有差别 test_res = test_data * resLogistic 回归
Logistic regression可以用来回归,也可以用来分类。比如,目前我们要判断某用户是否患有癌症,那么自变量只能有两个:0,1 分别表示是否患癌,因变量有很多。我们就需要一个函数,任意输入我们的因变量,输出 0 或 1 的结果。
这种情况下,线性回归是没法解决的;因为线性回归只能找出一堆数据中最拟合的回归系数,从而通过公式对新的值进行预测。
而我们现在需要的是通过算法,找到不同分类数据的边界,得到边界处各个系数,然后通过公式对新的值进行计算,把结果和边界处的值进行比较,大于的则判定它属于分类1,小于边界处值的则判定它属于分类2。
从这个逻辑上来看,这属于一个二项分布。而二项分布的分布律是:P(y) = py * (1-p)1-y
对于边界线,我们可以知道它的函数是:F(x) = wTx = 0 并且,这条边界线上的点,属于两边的概率是一样的,即:
P(Y = 1 | x) / P(Y = 0 | x) = 1且有:P(Y = 1 | x) + P(Y = 0 | x) = 1我们将该等式
P(Y = 1 | x) / P(Y = 0 | x) = 1变换一下,就变成了:ln(P(Y = 1 | x) / P(Y = 0 | x)) = 0由于 wTx = 0, 将等式右侧的 0 进行替换:
==>ln(P(Y = 1|x) / P(Y = 0|x)) = wTx
由于
P(Y = 1 | x) + P(Y = 0 | x) = 1, 可以得知P(Y = 1 | x) = 1 - P(Y = 0 | x)将等式左侧进行替换:==>ln(P(Y = 1 | x) / (1- P(Y = 1 | x))) = wTx
==>ewTx = P(Y = 1 | x) / (1- P(Y = 1 | x))
P(Y = 1 | x)的意思是某点的结果是 1 的概率,我们简化为 P==>ewTx = P / (1 - P)
==> P = (1 - P)ewTx
==> P = ewTx - P * ewTx
==> P(1 + ewTx) = ewTx
==> P = ewTx / (1 + ewTx)
==> P = 1 / (1 + e-wTx)
注意,上面的推导是专门针对边界线上的点进行的。我们观察上面的等式。分母中 wTx</sup> 就是直线的表达式。那么,我们就可以知道,无论边界是不是直线,只要它能用函数表达式出,就能使用上面的等式。
即,上面的等式可以简化为:
P = 1 / (1 + e-z)
其中,z 就是边界线的函数表达式。
上面的函数就是 Logistic 回归的描述函数了
该函数的曲线是:
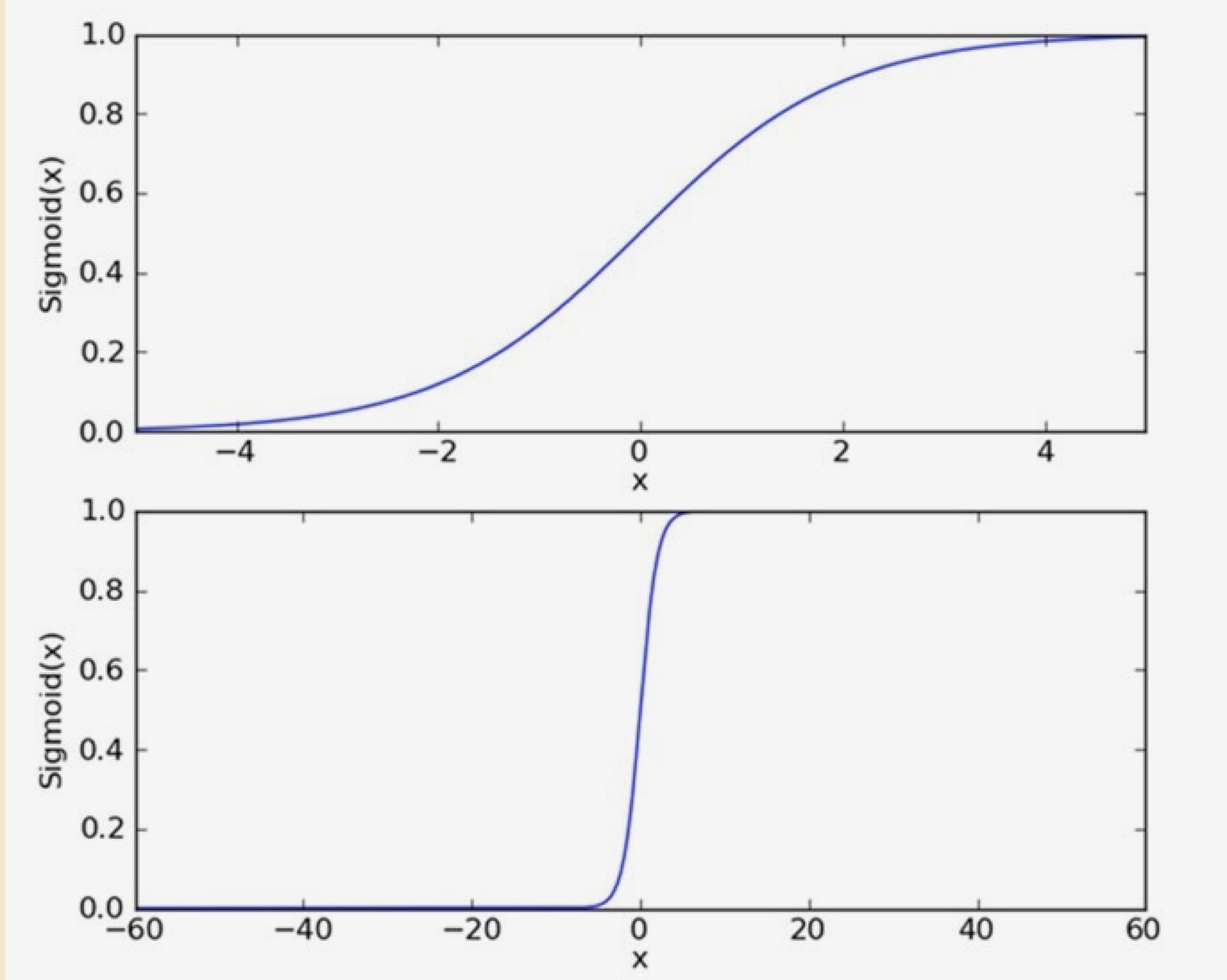
它将无穷的值映射到了(0,1), 描述的是属于类别 1 的概率。对于 z = 0 的点,就是前面提到的分界线上的点,函数值是 0.5,表示它属于类别 1 的概率是 0.5,于是它属于类别 2 的概率也是 0.5。
那么,剩下的任务就是如何找到边界,确定边界的函数了。对于直线分隔的两个分类,函数就是 wTx,而该函数里要确定的就是各个参数的值:w。
梯度上升算法求边界
前面已经知道该公式:
y = w0+w1x1+⋯+wnxn
我们将它简化成: y = wTx。x 是各个因变量的值,w 就是我们要得到的各个因变量的权重。也称最佳系数。我们需要找到最合适的系数,让这个公式表示的直线正好把不同分类的数据分隔开。即:这条线是不同数据的边界。
这里我们使用梯度上升算法来判断边界在何处。思路是:要找到某函数的最大值,最好的方法就是沿着该函数的梯度方向探寻。
案例:
给定一个样本集,每个样本点有两个维度值(X1,X2)和一个结果值,结果只有两种,我们以 0 和 1 代表。数据如下所示:
样本 x1 x2 结果 1 -1.4 4.7 1 2 -2.5 6.9 0 机器学习的任务是找一个函数,给定一个数据两个维度的值,该函数能够预测其结果为 1 的概率。 这个函数的模样如下:
h(x) = sigmoid(z)
z = w0 + w1 * X1 + w2 * X2
现在,问题转化成了: 根据现有的样本数据,找出最佳的参数 w(w0,w1,w2)的值。
假设现在手上已经有一个函数h(x),那么我们可以把样本1和样本2的数据代进去,看看这个函数的预测效果如何,假设样本1的预测值是p1 = 0.8,样本2的预测值是:p2 = 0.4。
函数在样本1上犯的错误为e1=(1-0.8)= 0.2,在样本2上犯的错误为e2=(0-0.4)= -0.4,总的错误 E 为 -0.20(e1+e2)。如下表所示:
样本 x1 x2 结果 预测值 误差 1 -1.4 4.7 1 0.8 0.2 2 -2.5 6.9 0 0.4 -0.4 知道了算法的误差,我们就需要改进算法,让误差尽量小。通常,评判误差值的方法有很多种,叫作损失函数,如:平方损失函数,对数损失函数。
平方损失函数是用最小二乘法,它的原理是中心极限定律,将每个测试数据预测值和实际值的差值求平方然后再累加。即: L(yi, f(xi)) = ∑(yi - f(xi))2 在线性回归算法中,我们就是用平方损失函数来判断直线是否最拟合的。且,损失函数中的 f(x) = wTx
对数损失函数的原理是极大似然估计。
对于样本 1 来说: 我们的预测值比理论值小,所以我们要提高函数输出的值。即提高 w1 * X1 的值。由于 X1 是负数,所以我们要达到目标,必须减少 w1 的值。
对于样本 2 来说: 我们的预测值比理论值大,所以我们要减少函数输出。即减小 w1 * X1 的值。由于 X1 是负数,为了达到目标,必须增大 w1 的值。
同样的算法,对样本1来说,调高系数会让算法更准确;对样本2,调低系数会更准确。这时候,我们就要进行取舍,看怎么调整会让最终的结果更准确。比如:调高后,样本1 的错误大大减少,样本2 的错误稍微增加,那么就可以调高。具体要增加多少,可以用一个变量 alpha 来表示,通过一次次的非常微小的调整来进行尝试。当最终的准确度达到最高后,终止尝试。这种做法就叫:梯度上升法,我们找到函数的最大值。我们也可以通过调低的方式来进行调整,这样我就找的就是最小值,那就叫:梯度下降法
画决策边界
现有如下数据集:
-0.017612 14.053064 0 -1.395634 4.662541 1 -0.752157 6.538620 0 -1.322371 7.152853 0 0.423363 11.054677 0 0.406704 7.067335 1有 100 个样本数据坐标点。第一列表示横坐标,第二列是纵坐标,第三列表示点的类型。这里用颜色区分,1 表示是红色,0 表示蓝色。这些点在坐标系中如下图:
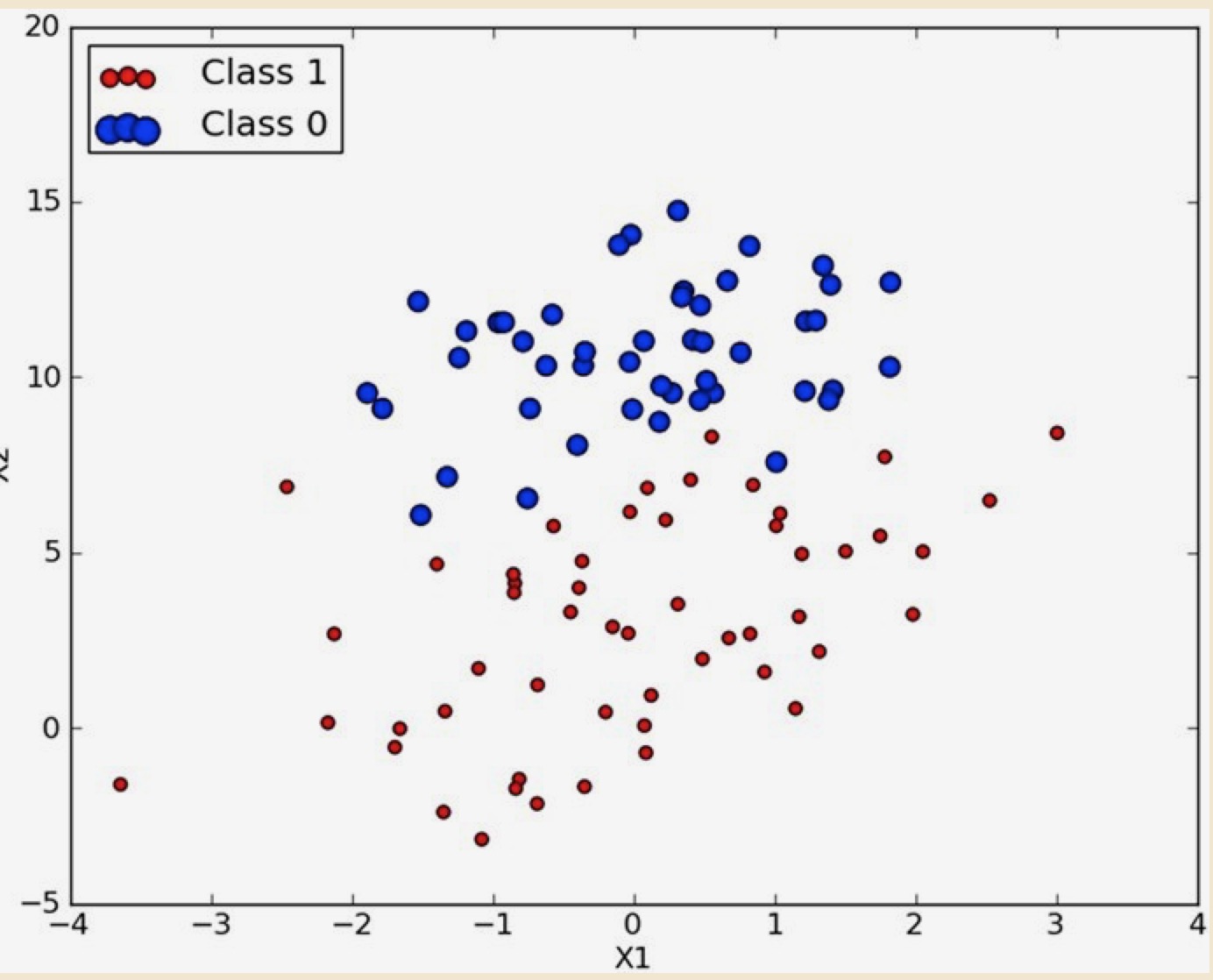
现在想要:给出一个点的坐标,预测他是红还是蓝。将问题转换一下,就是:找出红蓝的边界线。然后找出该点的横坐标处的边界的纵坐标。如果点的纵坐标大于边界纵坐标,点就是蓝色,反之是红色。
代码如下:
# -*- coding: utf-8 -*- from numpy import * # 加载测试数据.将 csv 格式的数据读取到多维数组中. # 数组的每一个值又是一个数组。数组的第一个值是1.0,因为后面的矩阵运算会用乘法,而公式中规定: p = w0 + w1 * x1 + w2 * x2 ... wn * xn # w0 是固定的值,不能在运算时变化,所以这里给矩阵引入一个 x0, 且值为 1 # 公式就变为: p = w0 * x0 + w1 * x1 + w2 * x2 ... wn * xn, 且x0 = 1 # 后面两个值是测试数据的头两行,即横坐标和纵坐标 # 数据中的结果单独在一个数组中 def loadDataSet(): dataMat = []; labelMat = [] fr = open('testSet.txt') for line in fr.readlines(): lineArr = line.strip().split() dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) labelMat.append(int(lineArr[2])) return dataMat, labelMat # sigmoid 算法.将值归到 0 - 1 之间.它是随输入值变大页递增的 # 当 x = 0 时,Sigmoid 的值是 0.5;x 越大,值越逼近 1。x 越小,值越逼近 0。 def sigmoid(inX): return 1.0/(1+exp(-inX)) # 算出回归系数 # 回归算法: y = w0+w1x1+⋯+wnxn ; w0 是固定值 def gradAscent(dataMatIn, classLabels): # 数组转换为矩阵.大小是 100 * 3 dataMatrix = mat(dataMatIn) # 数组转矩阵.大小是 100 * 1 labelMat = mat(classLabels).transpose() # 测试数据矩阵的形状.测试数据是 100 条,加载数据时每一行的长度又是 3 # 所以这里 m = 100; n = 3 m, n = shape(dataMatrix) # 在递增测试时,给出一个一次加多少的系数 alpha = 0.001 # 循环多少次,以找到函数的最优系数 maxCycles = 500 # 初始值.是一个 3 x 1 的矩阵.就是 w0, w1, w2 # w0 表示算法中固定的值.w1 表示数据坐标点横坐标的系数; w2 表示数据坐标点纵坐标的系数; # 后面会在算法中对该矩阵进行 N 次的微调 weights = ones((n, 1)) # 循环找边界 for k in range(maxCycles): # 计算当前的函数输出值 h = sigmoid(dataMatrix * weights) # 计算当前算法的误差值。 # 从数学角度来说,边界线的函数是 f(x, w) = w1x1 + w2x2 + ... + wnxn = wTx, w 就是参数矩阵,就是这里的 weights # 如果差值大于 0,表示建模的函数值比较实际的要小,需要把参数调大;如果有效期值小于 0,则要把参数调小。 error = (labelMat - h) # 根据误差调整参数.如果差值大于 0,这里的运算会把参数调高; weights = weights + alpha * dataMatrix.transpose() * error return weights # 画边界 def plotBestFit(weights): import matplotlib.pyplot as plt # 加载数据 dataMat,labelMat = loadDataSet() dataArr = array(dataMat) # 数据条数 n = shape(dataArr)[0] xcord1 = []; ycord1 = [] xcord2 = []; ycord2 = [] # 遍历数据.将各个数据按最后一列的值分类存放 for i in range(n): if int(labelMat[i])== 1: xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) else: xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2]) fig = plt.figure() ax = fig.add_subplot(111) # 添加各个坐标点.并按类别显示不同的颜色 ax.scatter(xcord1, ycord1, s=30, c='red', marker='s') ax.scatter(xcord2, ycord2, s=30, c='green') x = arange(-3.0, 3.0, 0.1) # 分界线的位置.我们判断时的标准是:函数得到的值小于 0.5, 则认为它是结果 0;大于 0.5 认为是结果 1.所以,边界处的函数值是 0.5. # 由于边界值是经过 sigmoid 计算过的.而 0.5 对应 sigmoid 之前的值是 0,即此处 w0 + w1x1 + w2x2 的值是 0 # 由此,先定义一个概念:边界处的函数输出值是 0 # 0 = w0 + w1x1 + w2x2 就是边界线的方程.w0, w1, w2 已经在 weights 数组中 # x1 是横坐标, x2 是纵坐标.所以 x2 = (-w0 - w1x1) / w2 y = (-weights[0] - weights[1] * x) / weights[2] ax.plot(x, y) plt.xlabel('X1'); plt.ylabel('X2'); plt.show() # 加载测试数据 data, label = loadDataSet() res = gradAscent(data, label) plotBestFit(res.getA())运行后生成图:
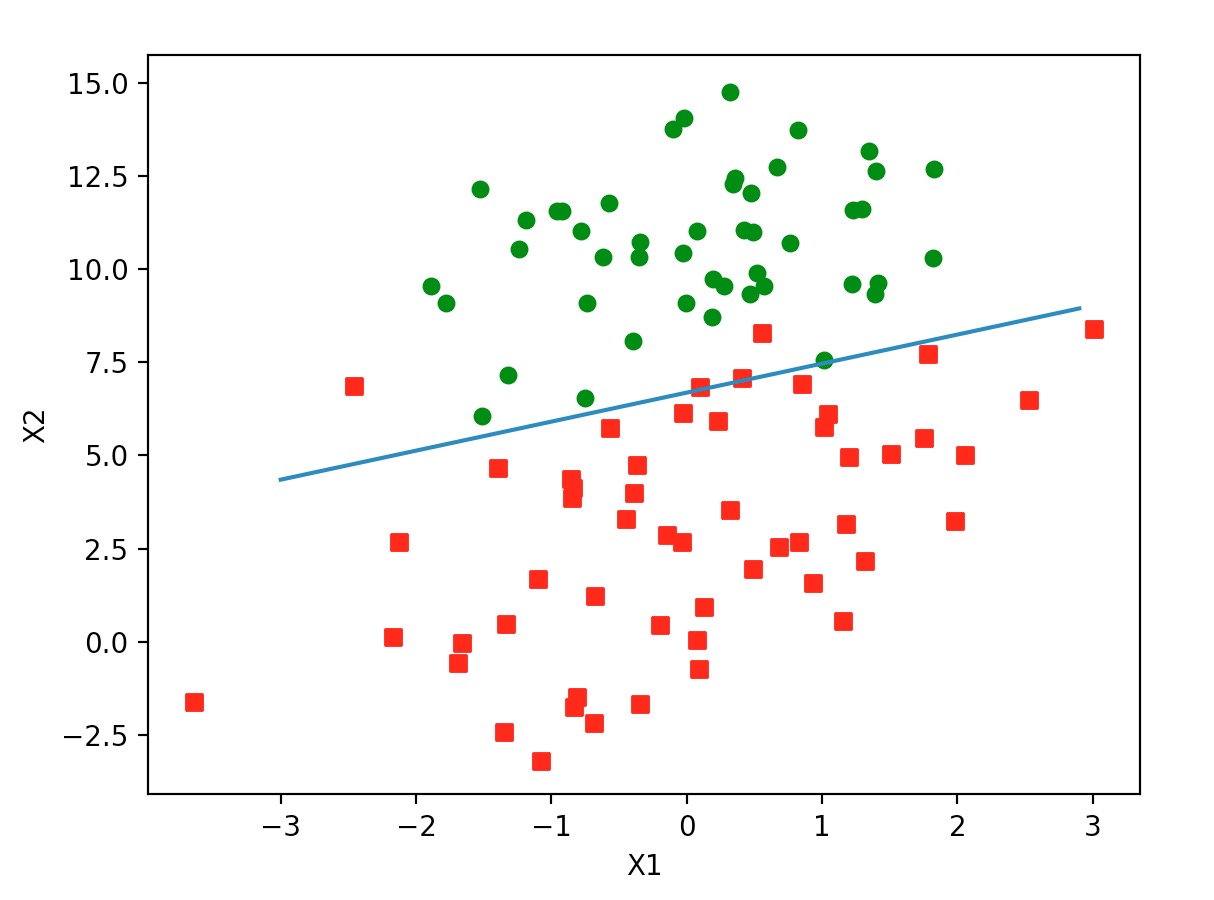
从图中可以看到只有少数几个点是被错误划分了。说明准确率还是不错的。但通过代码我们可以看到。在 500 次的循环中,每次都要对整个数据矩阵进行运算。矩阵是 100 * 3 的,即每个循环都要进行 300 次乘法运算。如果数据量非常大,这就很慢了,而且消耗资源巨大。一种改进办法是:一次只对一个样本数据进行运算。代码如下:
# -*- coding: utf-8 -*- from numpy import * # 加载测试数据.将 csv 格式的数据读取到多维数组中. # 数组的每一个值又是一个数组。数组的第一个值是1.0,因为后面的矩阵运算会用乘法,而公式中规定: p = w0 + w1 * x1 + w2 * x2 ... wn * xn # w0 是固定的值,不能在运算时变化,所以这里给矩阵引入一个 x0, 且值为 1 # 公式就变为: p = w0 * x0 + w1 * x1 + w2 * x2 ... wn * xn, 且x0 = 1 # 后面两个值是测试数据的头两行,即横坐标和纵坐标 # 数据中的结果单独在一个数组中 def loadDataSet(): dataMat = []; labelMat = [] fr = open('testSet.txt') for line in fr.readlines(): lineArr = line.strip().split() dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) labelMat.append(int(lineArr[2])) return dataMat, labelMat # sigmoid 算法.将值归到 0 - 1 之间.它是随输入值变大页递增的 # 当 x = 0 时,Sigmoid 的值是 0.5;x 越大,值越逼近 1。x 越小,值越逼近 0。 def sigmoid(inX): return 1.0/(1+exp(-inX)) def stocGradAscent1(dataMatrix, classLabels, numIter=150): m, n = shape(dataMatrix) weights = ones(n) for j in range(numIter): dataIndex = range(m) for i in range(m): # 动态调整系数.会随着运行减少,但永远不会减少到 0。这样就保证了该值对最后的结果是有影响的,而且它的正负性质不会改变 # 也可以自己定义一个算法 alpha = 4/(1.0+j+i)+0.0001 # 每次随机取一个样本来计算 randindex = int(random.uniform(0, len(dataIndex))) h = sigmoid(sum(dataMatrix[randindex] * weights)) error = classLabels[randindex] - h # 根据不同参数来调整系数.这里 alpha, error 成为了数值, 不是向量;这就又减少了运算量 # 对参数的处理方式和之前一样。如果差值大于 0,表示建模的函数值比较实际的要小,需要把参数调大;如果有效期值小于 0,则要把参数调小。 weights = weights + alpha * error * dataMatrix[randindex] # 为保证调整后下次不再取到它,把它从列表中删除 del(dataIndex[randindex]) return weights # 画边界 def plotBestFit(weights): import matplotlib.pyplot as plt # 加载数据 dataMat,labelMat = loadDataSet() dataArr = array(dataMat) # 数据条数 n = shape(dataArr)[0] xcord1 = []; ycord1 = [] xcord2 = []; ycord2 = [] # 遍历数据.将各个数据按最后一列的值分类存放 for i in range(n): if int(labelMat[i])== 1: xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) else: xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2]) fig = plt.figure() ax = fig.add_subplot(111) # 添加各个坐标点.并按类别显示不同的颜色 ax.scatter(xcord1, ycord1, s=30, c='red', marker='s') ax.scatter(xcord2, ycord2, s=30, c='green') x = arange(-3.0, 3.0, 0.1) # 分界线的位置.我们判断时的标准是:函数得到的值小于 0.5, 则认为它是结果 0;大于 0.5 认为是结果 1.所以,边界处的函数值是 0.5. # 由于边界值是经过 sigmoid 计算过的.而 0.5 对应 sigmoid 之前的值是 0,即此处 w0 + w1x1 + w2x2 的值是 0 # 由此,先定义一个概念:边界处的函数输出值是 0 # 0 = w0 + w1x1 + w2x2 就是边界线的方程.w0, w1, w2 已经在 weights 数组中 # x1 是横坐标, x2 是纵坐标.所以 x2 = (-w0 - w1x1) / w2 y = (-weights[0] - weights[1] * x) / weights[2] ax.plot(x, y) plt.xlabel('X1'); plt.ylabel('X2'); plt.show() # 加载测试数据 data, label = loadDataSet() res = stocGradAscent(array(data), label) plotBestFit(res)案例:疝气病症预测病马的死亡率
目前我们已经有了梯度上升的算法 stocGradAscent(dataMatrix, classLabels, numIter=150) ,它可以接受一个数据集合,结果集合,和遍历次数。就可以求出最佳系数的集合。那么,我们就可以用它来进行预测,逻辑是:
- 拿到一些数据进行训练,得到最佳系数。
- 拿到需要测试的数据,把系数和数据带入公式中,计算回归值。
- 把回归值进行 Sigmoid 运算,得到的值和 0.5 进行比较,以判断结果。
训练数据:
2.000000 1.000000 38.500000 66.000000 28.000000 3.000000 3.000000 0.000000 2.000000 5.000000 4.000000 4.000000 0.000000 0.000000 0.000000 3.000000 5.000000 45.000000 8.400000 0.000000 0.000000 0.000000 1.000000 1.000000 39.200000 88.000000 20.000000 0.000000 0.000000 4.000000 1.000000 3.000000 4.000000 2.000000 0.000000 0.000000 0.000000 4.000000 2.000000 50.000000 85.000000 2.000000 2.000000 0.000000 2.000000 1.000000 38.300000 40.000000 24.000000 1.000000 1.000000 3.000000 1.000000 3.000000 3.000000 1.000000 0.000000 0.000000 0.000000 1.000000 1.000000 33.000000 6.700000 0.000000 0.000000 1.000000 1.000000 9.000000 39.100000 164.000000 84.000000 4.000000 1.000000 6.000000 2.000000 2.000000 4.000000 4.000000 1.000000 2.000000 5.000000 3.000000 0.000000 48.000000 7.200000 3.000000 5.300000 0.000000 2.000000 1.000000 37.300000 104.000000 35.000000 0.000000 0.000000 6.000000 2.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 74.000000 7.400000 0.000000 0.000000 0.000000 2.000000 1.000000 0.000000 0.000000 0.000000 2.000000 1.000000 3.000000 1.000000 2.000000 3.000000 2.000000 2.000000 1.000000 0.000000 3.000000 3.000000 0.000000 0.000000 0.000000 0.000000 1.000000 1.000000 1.000000 37.900000 48.000000 16.000000 1.000000 1.000000 1.000000 1.000000 3.000000 3.000000 3.000000 1.000000 1.000000 0.000000 3.000000 5.000000 37.000000 7.000000 0.000000 0.000000 1.000000 1.000000 1.000000 0.000000 60.000000 0.000000 3.000000 0.000000 0.000000 1.000000 0.000000 4.000000 2.000000 2.000000 1.000000 0.000000 3.000000 4.000000 44.000000 8.300000 0.000000 0.000000 0.000000 2.000000 1.000000 0.000000 80.000000 36.000000 3.000000 4.000000 3.000000 1.000000 4.000000 4.000000 4.000000 2.000000 1.000000 0.000000 3.000000 5.000000 38.000000 6.200000 0.000000 0.000000 0.000000 2.000000 9.000000 38.300000 90.000000 0.000000 1.000000 0.000000 1.000000 1.000000 5.000000 3.000000 1.000000 2.000000 1.000000 0.000000 3.000000 0.000000 40.000000 6.200000 1.000000 2.200000 1.000000测试数据:
2 1 38.50 54 20 0 1 2 2 3 4 1 2 2 5.90 0 2 42.00 6.30 0 0 1 2 1 37.60 48 36 0 0 1 1 0 3 0 0 0 0 0 0 44.00 6.30 1 5.00 1 1 1 37.7 44 28 0 4 3 2 5 4 4 1 1 0 3 5 45 70 3 2 1 1 1 37 56 24 3 1 4 2 4 4 3 1 1 0 0 0 35 61 3 2 0 2 1 38.00 42 12 3 0 3 1 1 0 1 0 0 0 0 2 37.00 5.80 0 0 1 1 1 0 60 40 3 0 1 1 0 4 0 3 2 0 0 5 42 72 0 0 1 2 1 38.40 80 60 3 2 2 1 3 2 1 2 2 0 1 1 54.00 6.90 0 0 1 2 1 37.80 48 12 2 1 2 1 3 0 1 2 0 0 2 0 48.00 7.30 1 0 1代码如下:
def classifyVector(inX, weights): # 计算回归值,然后再计算 sigmoid 的值 prob = sigmoid(sum(inX*weights)) # 根据 sigmoid 的值进行预测 if prob > 0.5: return 1.0 else: return 0.0 def colicTest(): # 训练用的数据 frTrain = open('horseColicTraining.txt') # 待测试的数据 frTest = open('horseColicTest.txt') trainingSet = []; trainingLabels = [] # 遍历训练数据.对于某些缺少数值的列,我们可以用 0 来填充. # 用 0 填充后,后面梯度上升算法计算系数时 weights = weights + alpha * error * dataMatrix[randindex], 权重会不变,这样对结果就不会产生影响 for line in frTrain.readlines(): currLine = line.strip().split('\t') lineArr =[] for i in range(21): lineArr.append(float(currLine[i])) trainingSet.append(lineArr) # 数据最后一列是结果 trainingLabels.append(float(currLine[21])) # 计算最优系数.进行 1000 次计算 trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 1000) errorCount = 0; numTestVec = 0.0 # 开始测试系数准确度 for line in frTest.readlines(): numTestVec += 1.0 currLine = line.strip().split('\t') lineArr =[] for i in range(21): lineArr.append(float(currLine[i])) if int(classifyVector(array(lineArr), trainWeights)) != int(currLine[21]): errorCount += 1 errorRate = (float(errorCount)/numTestVec) print "预测错误率是: %f" % errorRate return errorRate colicTest()
-
决策树
决策树
决策树是最经常使用的数据挖掘算法。它的重要任务就是找出数据中蕴含的信息,从数据集合中撮一系列规则,机器根据数据创建规则的过程就是机器学习的过程。
案例:测试患者要佩戴的隐形眼镜类型
使用较小的训练数据集,我们可以让算法掌握一套判断流程(决策数):眼科医生是如何判断患者要佩戴眼镜的类型的。
训练数据集中包括过往的一些诊断结果。包含患者眼部状况(散光、),医生推荐的眼镜类型(眼镜材质,是否适合隐形眼镜)等。
数据如下:
young myope no reduced no lenses young myope no normal soft young myope yes reduced no lenses young myope yes normal hard young hyper no reduced no lenses young hyper no normal soft young hyper yes reduced no lenses young hyper yes normal hard pre myope no reduced no lenses pre myope no normal soft pre myope yes reduced no lenses pre myope yes normal hard pre hyper no reduced no lenses pre hyper no normal soft pre hyper yes reduced no lenses pre hyper yes normal no lenses presbyopic myope no reduced no lenses presbyopic myope no normal no lenses presbyopic myope yes reduced no lenses presbyopic myope yes normal hard presbyopic hyper no reduced no lenses presbyopic hyper no normal soft presbyopic hyper yes reduced no lenses presbyopic hyper yes normal no lenses第一列表示患者年龄,第二列表示诊断说明,第三列表示是否有散光,第四列表示是否能够接受隐形眼镜,第五列表示最终的结果。
看似无规律的数据,我们可以通过程序进行总结,找出规律。比如:是否能接受隐形眼镜,如果 拒绝(第四列为 reduce),结果直接就为 no lenses; 如果是能接受(第四列是 normal),进一步判断是否有散光(第三列值)。如果没有散光,再判断年龄(第一列)…等等。
其实,程序是根据我们数据各个列的意义来做为判断的依据。但有个问题是:哪一列作为最优先的判断。比如上面说的,为什么要先判断是否能接受隐形眼镜?而不是先判断年龄。
程序是通过“信息增益”来进行判断的,原则就是对最终结果的影响是多少(专业术语叫:熵)。于是,我们就可以计算每一列对结果的总影响是多少。影响越大的,我们越放在前面进行判断。
用数学公式表示: l(xi)=-log2p(xi)
思路: 从数据可以看出,前四列是各项指标;最后一列是在各个指标组合下的结果。 那么,就可以先整体计算一下全体数据的熵。然后分别减去某一列,再次计算熵。两者差值越大,表示该列对结果影响越大。那么,它的判断优先度就应该越高,即:它就是决策树的第一个节点。
代码:
# -*- coding: utf-8 -*- from math import log import operator decisionNode = dict(boxstyle="sawtooth", fc="0.8") leafNode = dict(boxstyle="round4", fc="0.8") arrow_args = dict(arrowstyle="<-") def majorityCnt(classList): classCount = {} for vote in classList: if vote not in classCount.keys(): classCount[vote] = 0 classCount[vote] += 1 sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True) return sortedClassCount[0][0] # 划分数据集. # dataSet: 待划分的数据集 # axis: 列数.以哪一列来划分数据集 # values: 需要返回的特征值 def splitDataSet(dataSet, axis, value): retDataSet = [] # 遍历数据每一行。得到每一行的向量 for featVec in dataSet: # 如果当前行向量的待划分列的值和需要返回的特征值相同,表示该行数据是我们需要的。 # 将该列去掉(取前N列和后面的几列,重新组合成数据集) if featVec[axis] == value: reducedFeatVec = featVec[:axis] reducedFeatVec.extend(featVec[axis + 1:]) retDataSet.append(reducedFeatVec) return retDataSet # 计算香农值 def calcShannonEnt(dataSet): numEntries = len(dataSet) labelCounts = {} # 最终结果(标签)的唯一列表 for featVec in dataSet: currentLabel = featVec[-1] if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 labelCounts[currentLabel] += 1 shannonEnt = 0.0 for key in labelCounts: prob = float(labelCounts[key]) / numEntries shannonEnt -= prob * log(prob, 2) return shannonEnt def chooseBestFeatureToSplit(dataSet): # 属性(待划分数据集的依据)的个数.由于最后一列是标签,或者叫分类,就是最终的结果。所以最后一列不用计算香农值 # 测试数据总共有 5 列,最后一列是结果。所以这里取前 4 列 numFeatures = len(dataSet[0]) - 1 # 整个数据集的香农值 baseEntropy = calcShannonEnt(dataSet) bestInfoGain = 0.0 bestFeature = -1 # 遍历每一列。因为要以每一列为依据来划分数据集。然后计算每一列和结果组合的香农值。以此来判断该列对结果的影响有多大 # 影响最大的在决策数的最顶部 for i in range(numFeatures): # 找到当前列所有的值 featList = [example[i] for example in dataSet] # 当前列的值去重 uniqueVals = set(featList) newEntropy = 0.0 # for value in uniqueVals: # 划分数据集.从原始数据集中去掉当前列,且只找当前列的值是遍历值的 # 作用是为了计算每一列,每个值对最终结果的影响 subDataSet = splitDataSet(dataSet, i, value) # 当前列,当前值占总数据的比例。相当于出现这种情况的概率 prob = len(subDataSet) / float(len(dataSet)) # 由于循环里是分别计算当前列各个值的香农植。所以将各个唯一值的香农值累加就是该列整体的香农值 newEntropy += prob * calcShannonEnt(subDataSet) # 由于计算的是当前列删除后的香农值。所以该列的实际值是用总的值减去该列的总值 infoGain = baseEntropy - newEntropy # 找到值最大的一列 if (infoGain > bestInfoGain): bestInfoGain = infoGain bestFeature = i return bestFeature # 创建决策树.程序会使用递归的方式来创建.每创建一层后,从数据集中去掉已经处理的列。将剩下的再进行分析。 # dataset: 数据集 # labels: 数据集每一列的含义(名称) def createTree(dataSet, labels): # 取数据集最后一列的值 classList = [example[-1] for example in dataSet] # 如果该列中所有的值都一样,直接返回 if classList.count(classList[0]) == len(classList): return classList[0] # 如果当前列表只有一列 if len(dataSet[0]) == 1: return majorityCnt(classList) # 找到对结果影响最大的一列。把它做为决策树的最顶部判断条件 bestFeat = chooseBestFeatureToSplit(dataSet) # 影响最大一列的名称(自定义的) bestFeatLabel = labels[bestFeat] # 定义一个树 myTree = {bestFeatLabel: {}} # 将影响最大的列从标签列表去除.后面需要将剩余的标签做进一步处理 del (labels[bestFeat]) # 最优列的所有值 featValues = [example[bestFeat] for example in dataSet] # 最优列值去重 uniqueVals = set(featValues) for value in uniqueVals: # 复制 labels ,然后使用,以免对原数据造成影响 subLabels = labels[:] # 递归调用本方法。传入的数据集是去掉当前最优列的集合。意思是从剩余的列中再找最优列,然后再处理。 # 通过调归方法,可以依次找到对结果影响最大的列 myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels) # 树的各个判断条件就是各列的名字。最终终止点就是数据集的最后一列对应的值。判断条件的值就是该列的值。 return myTree fr = open('lenses.txt') lenses = [inst.strip().split('\t') for inst in fr.readlines()] # 数据每一列的含义 lenseslabels = ['age', 'prescript', 'astigmatic', 'tearRate'] lenesTree = createTree(lenses, lenseslabels) print lenesTree输出的结果是:
{'tearRate': {'reduced': 'no lenses', 'normal': {'astigmatic': {'yes': {'prescript': {'hyper': {'age': {'pre': 'no lenses', 'presbyopic': 'no lenses', 'young': 'hard'}}, 'myope': 'hard'}}, 'no': {'age': {'pre': 'soft', 'presbyopic': {'prescript': {'hyper': 'soft', 'myope': 'no lenses'}}, 'young': 'soft'}}}}}}从结果可以看出判断的顺序:先判断 tearRate,如果是 reduced,直接返回 no lenses; 如果是 normal,进入下一步 astigmatic 的判断:如果是 yes,进一步判断 prescript…
我们把这串 json 格式格式化后会稍微清晰一点。当然,我们可以生成图片类似流程图,那就更直观了:
def getNumLeafs(myTree): numLeafs = 0 firstStr = myTree.keys()[0] secondDict = myTree[firstStr] for key in secondDict.keys(): if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes numLeafs += getNumLeafs(secondDict[key]) else: numLeafs += 1 return numLeafs def getTreeDepth(myTree): maxDepth = 0 firstStr = myTree.keys()[0] secondDict = myTree[firstStr] for key in secondDict.keys(): if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes thisDepth = 1 + getTreeDepth(secondDict[key]) else: thisDepth = 1 if thisDepth > maxDepth: maxDepth = thisDepth return maxDepth def plotNode(nodeTxt, centerPt, parentPt, nodeType): createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', xytext=centerPt, textcoords='axes fraction', va="center", ha="center", bbox=nodeType, arrowprops=arrow_args ) def plotMidText(cntrPt, parentPt, txtString): xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0] yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1] createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30) def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on numLeafs = getNumLeafs(myTree) #this determines the x width of this tree depth = getTreeDepth(myTree) firstStr = myTree.keys()[0] #the text label for this node should be this cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff) plotMidText(cntrPt, parentPt, nodeTxt) plotNode(firstStr, cntrPt, parentPt, decisionNode) secondDict = myTree[firstStr] plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD for key in secondDict.keys(): if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes plotTree(secondDict[key],cntrPt,str(key)) #recursion else: #it's a leaf node print the leaf node plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode) plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key)) plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD def createPlot(inTree): fig = plt.figure(1, facecolor='white') fig.clf() axprops = dict(xticks=[], yticks=[]) createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) #no ticks #createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses plotTree.totalW = float(getNumLeafs(inTree)) plotTree.totalD = float(getTreeDepth(inTree)) plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0; plotTree(inTree, (0.5,1.0), '') plt.show() # 加上前面生成树的相关代码 createPlot(lenesTree)生成的图如下:
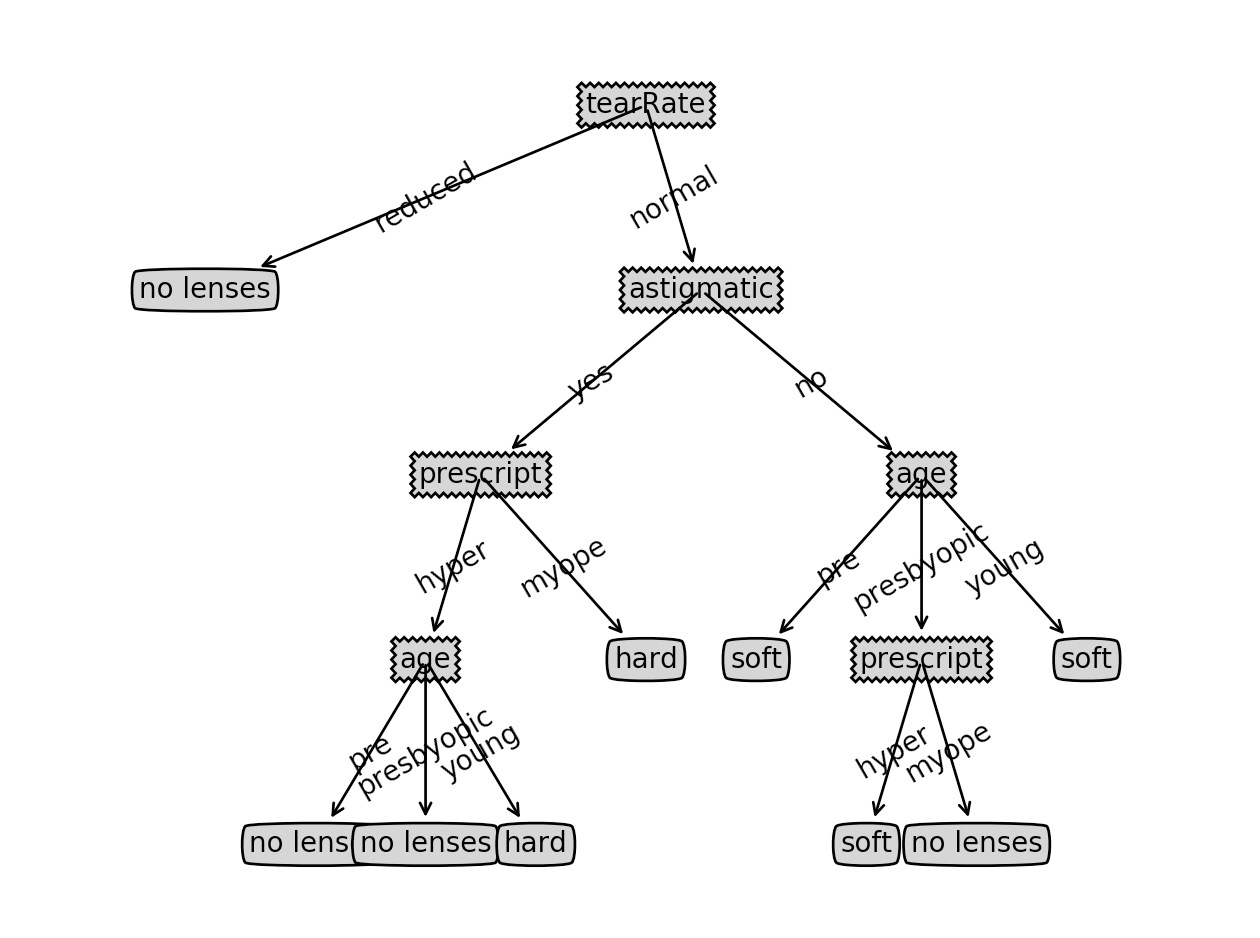
有了这个决策的逻辑,我们就可以对某种情况进行推断。比如现在有一位新患者,通过调查,我们知道他对各个判断指标的数值,那么我们就可以按上述判断逻辑走一遍,然后推算出他可能的结果。
-
svm
SVM 是目前最好的现成算法之一。它的好处是不用你做什么修改就可以直接使用。甚至不用理解它的原理。它和回归算法一样,也是用来进行数据的分类,求最优方式。
简单理解
现在桌子上有两种颜色(红色和蓝色)的球需要分类(如图),我们有一根棍子作为工具,如何才能准确的分类呢?

我们不用多考虑,直接把棍子放中间一放即可:
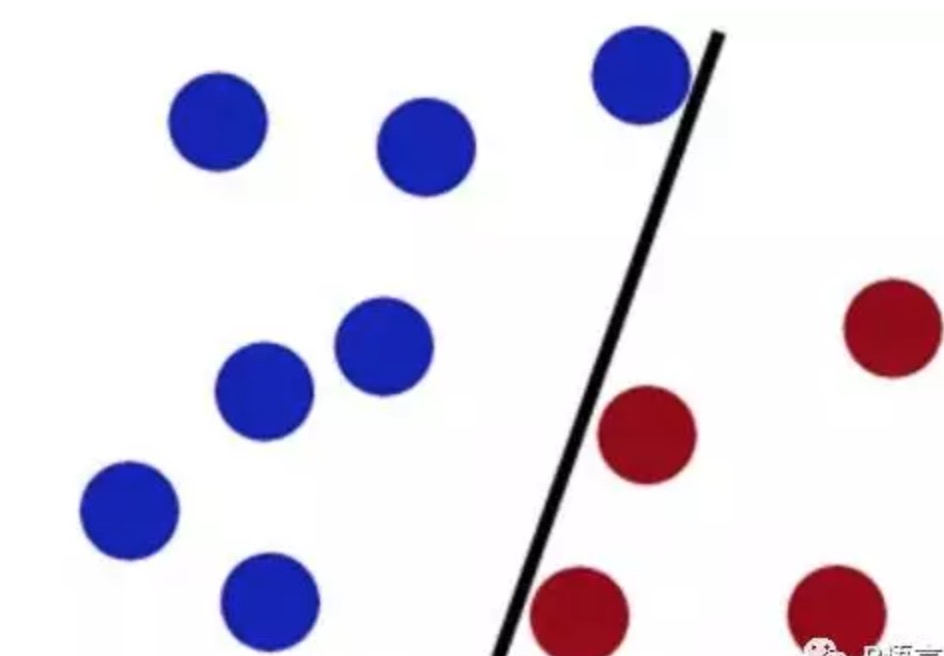
但如果这时候桌子上有更多的球,可能这个只能直线划分的棍子就不能完美的划分了,可能会有个别被划错。
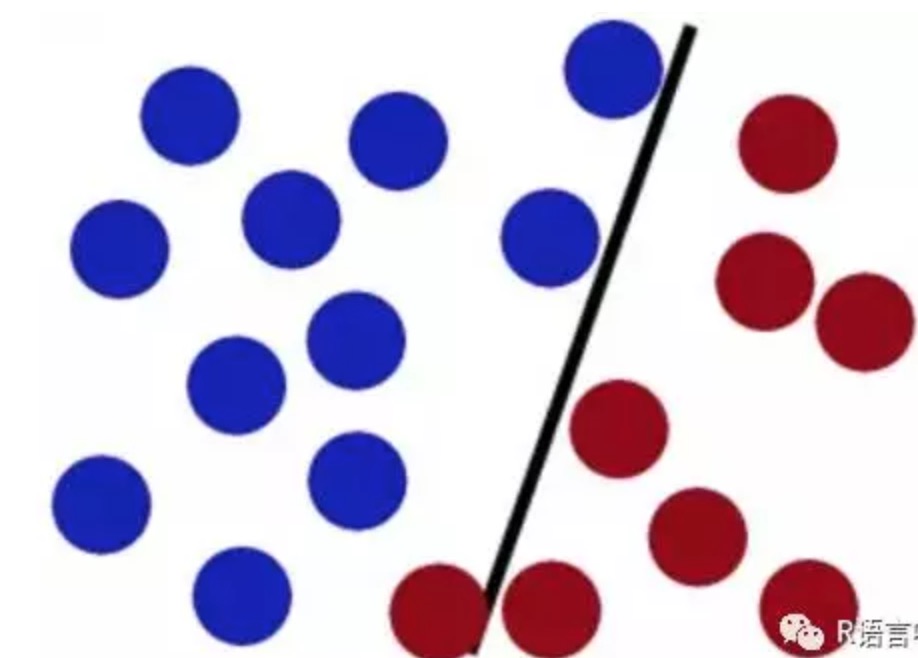
SVM便是将你手上的棍子放在最佳位置,这个最佳位置使得棍子两边的分类球有着最大的间隔
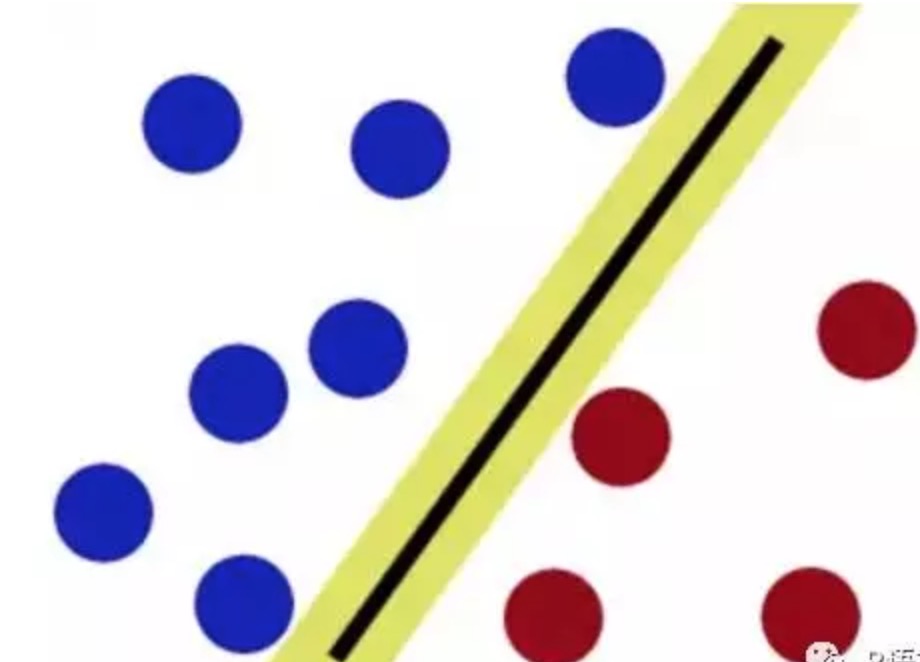
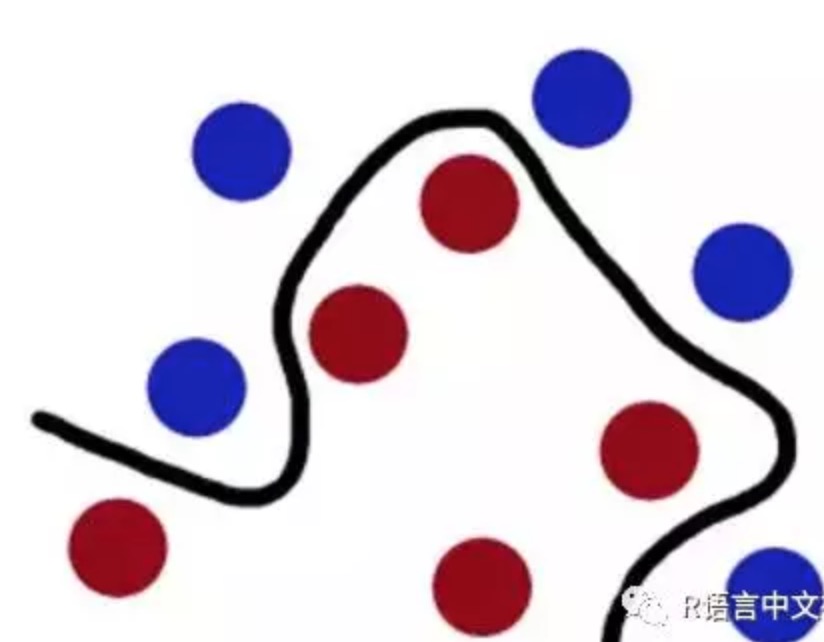
但是,如果两种颜色的球被混合到一起了。

用直直的棍子肯定就无法分隔了。这时候:猛地一拍桌子,所有的球顿时都飞到了空中,说时迟那时快,闪电般的抄起一张纸,刷的一下就飞到两种球中间,成功的将两种球分开了。
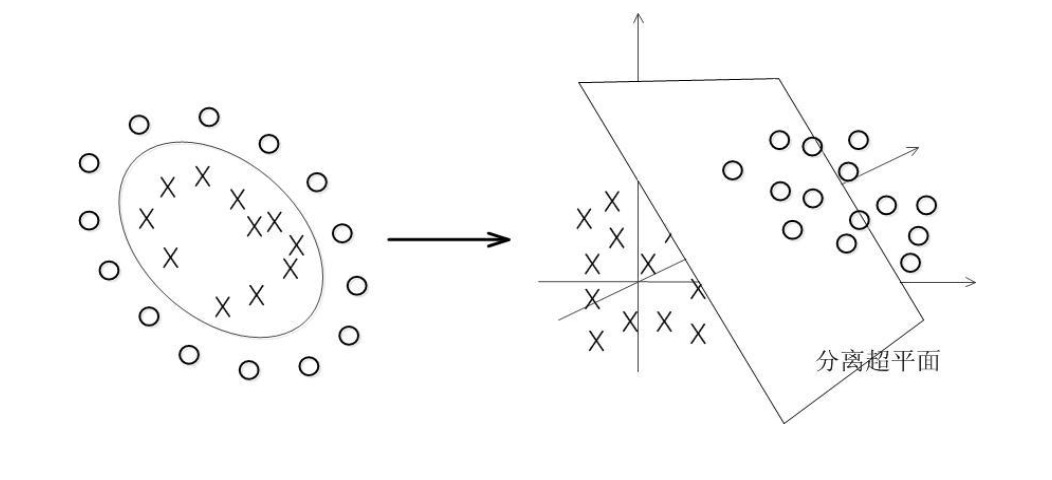
从平面上看,这些球就好像被一条曲线给分开了。
SVM算法中:这些球被称为数据,棍子被称之为分类器,使棍子两边间隔最大的方法叫做最优化,拍桌子那个技术被叫做核技术,那张被你抄向空中的纸叫做超平面,棍子由直线变成曲线便叫做软化。
在二维的空间中,我们需要做的是,找到一条线(一维),离两种球的距离都是最远。在三维空间中就是要找到一个面(二维),离两种球的距离都远。这里的二维,三维可以理解为实际应用中某事物的两个属性值或者三个属性值。即:我们要根据同一类事物同一属性不同的值,对事物进行区分。
既然是属性,就有可能有很多种,可能有成百上千个属性。比如 N 种,我们要找的实际上是一个 N-1 维的分界的超平面。
理论基础
svm 的目的是寻找一个超平面来对样本根据正例和反例进行分割。看上去象简单的线性回归。其实有非常大的区别。首先,SVM 要找出线性回归最优的情况;另外,非线性的时候也可以用SVM。
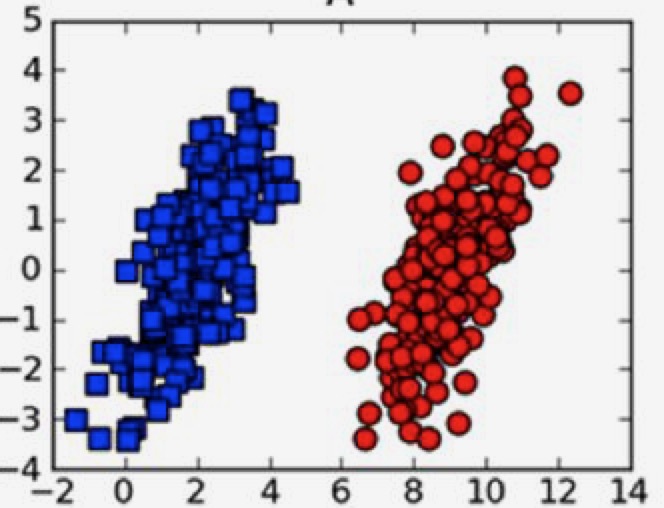
象这种,我们可以找出一条直线,把两种点完全分隔开,这种情况叫做线性可分。
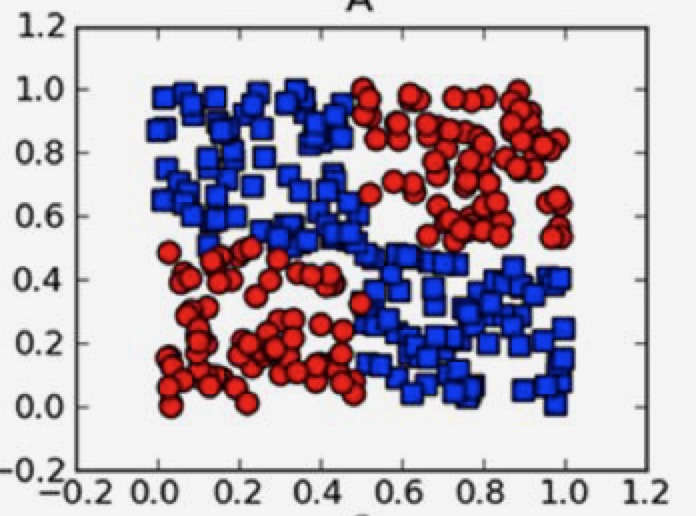
这种情况下,没法找出一条直线把两种点分隔,就叫线性不可分。
还有一种介于上面两种情况之间的状态:
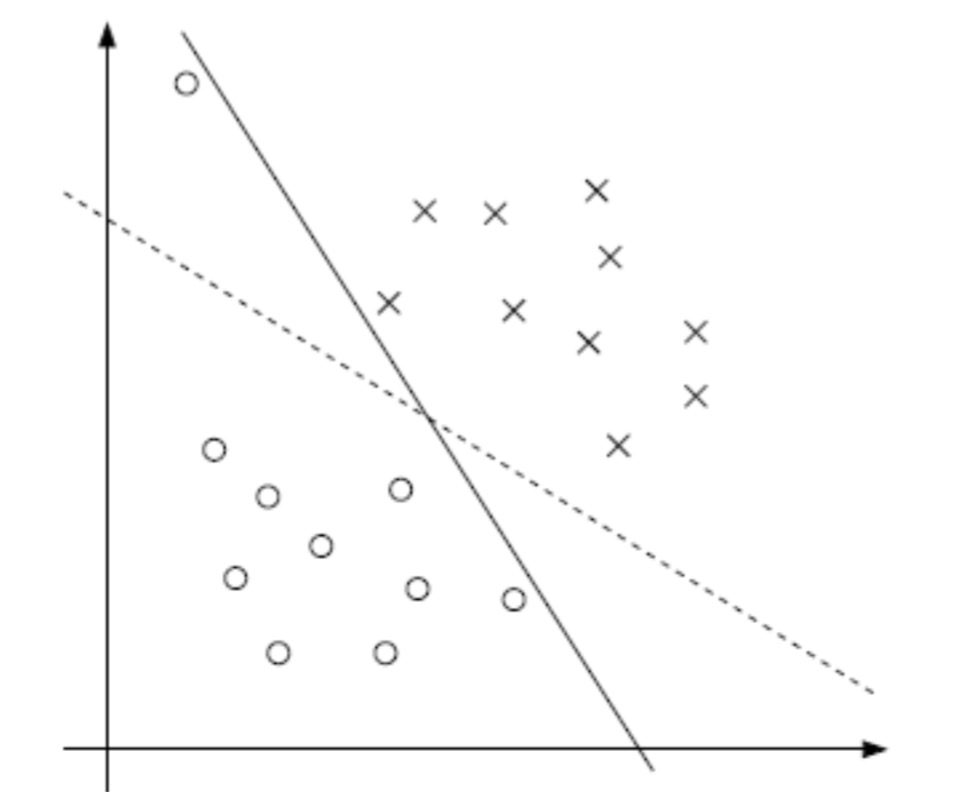
如图中虚线部分,看上去比实线更合理,但左上角有一个点是分错了的,但我们忽略掉这个点,选择虚线的划分算法。为了大多数的结果更准确。
SVM的核心思想是尽最大努力使分开的两个类别有最大间隔,这样才使得分隔具有更高的可信度。而且对于未知的新样本才有很好的分类预测能力(在机器学习中叫泛化能力)
那么怎么描述这个间隔,并且让它最大呢?SVM的办法是:让离分隔面最近的数据点具有最大的距离。
通俗的来说,我们可以这样:找出两个分类最近的两个点,在这两点上画出两条平行线;这两条线的中线就是分隔线。
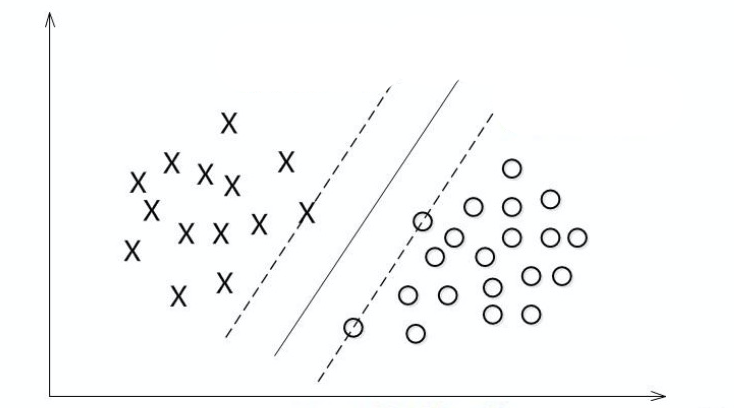
假定所有的点都满足这样的表达式:y = f(w, x);该函数返回的值是 -1 或 1,用来表示某点属于哪个分类。记得 logistic 回归里面,我们是将 0 和 1 做为两个不同分类的标记。这里则改成 1 和 -1 。这和SVM的处理方式是有关系的。因为SVM是要找出三条互相平行的线,左边一条表示属于分类 1 的点,最右边的表示属于分类 2 的点,中间的是边界线。所以,如果我们让左边的函数值为 1,右边的为 -1,正好中间的就是 0。这样方便计算,如果我们还使用 0 和 1,则中间边界线的值就是 1/2 了。
其实我们可以把函数的值定义成做任意值,比如 10,100;只不过这种情况下,w 和 b 的值稍有不同,会做一些等比例放大或缩小。如:w * x + b = 100,可以把它转换为:(w * x) / 100 + b/100 = 1,所以,我们可以把函数值定义为做任意的值。只是最终求出来的 w 和 b 不同。不过,为了求解方便,我们把值定义为 1 和 -1,让中间值是 0。而且 1 和 -1 在运算的时候只相当于一个正负号,就更方便了。
现在有这样的一个分隔线,它的函数表达式是 wTX + b; 那么,任意一个点到分隔线的距离就是 label * (wTX + b), 其中 label 表示它的类别,值是 1 或 -1。不管点是在分隔线的哪边,该距离会下都是正数,运算起来比较方便。
现在,我们就要通过这三条线,找出公式 y = f(wTX + b) 中的 w 和 b 的值。
H1: y = wTx + b = +1 和 H2: y = wTx + b = -1

在这两个超平面上的样本点也就是理论上离分隔超平面最近的点,是它们的存在决定了H1和H2的位置,支撑起了分界线,它们就是所谓的支持向量,这就是支持向量机名称的由来。
有了这两个超平面就可以顺理成章的定义上面提到的间隔(margin)了,二维情况下 ax+by=c1和 ax+by=c2 两条平行线的距离公式为:
( |C1 - C2| ) / ( √a2 + b2 )
在这里,c1 = 1, c2 = -1。所以,距离 m = 2 / ( √a2 + b2 ) = 2 / ||w||
||w||: 范数,结果为w向量的各个元素的平方和的开平方
注意:上面的 label * (wTX + b) 是函数距离。不是几何距离。比如,我们同时缩小或放大几倍 w 和 b,该函数没有变化,但计算的函数距离即变了。所以我们要用几何距离来代替,即:label * (wTX + b) / ||w||。这里涉及到平面几何的推导。
H1和H2两个超平面的间隔为 2 / ||w||,即现在的目的是要最大化这个间隔。等价于求最小化 ||w||,为了之后的求导和计算方便,进一步等价于最小化 1/2 * ||w||2, 因为如果 1/2 * ||w||2 最小,||w|| 肯定是最小。不过,转换后我们计算起来要更方便。
根据上面的分类,则有:
wTxi + b >= 1, yi = 1
wTxi + b <= -1, yi = -1
只有有线 h1 和 h2 上的值才等于 1 和 -1,而其它的点对应的值则是 >1 或 <-1
不等式综合起来就是:
yi(wTxi + b) -1 >= 0
那么,现在的问题就变成了: 在 yi(wTxi + b) -1 >= 0 条件下,求 1/2 * ||w||2 的最小值。在它取最小值的时候,w 和 b 的值就是我们需要的最佳系数。这时候,wTx + b = 0 是分割线的函数表达式。
这里可以用拉格朗日乘子法,它是专门用来解决函数在约束条件下极值的。通过求解与原问题等价的对偶问题(dual problem)得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:一者对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。
那什么是拉格朗日对偶性呢?简单来讲,通过给每一个约束条件加上一个拉格朗日乘子(Lagrange multiplier)α, 将约束条件融合到目标函数里去,从而只用一个函数表达式便能清楚的表达出我们的问题。上面的约束条件和求极值整合为:
L(w, b, a) = 1/2 * ||w||2 - ∑αi(yi(wTxi + b) - 1)
对 w 和 b 求偏导,得到: w = ∑αiyixi
这里就可以看出:如果 α 为 0,则不管 x 取什么值,都不会影响结果;也就是说 α 为 0 的这些点是非支撑向量。也就是说,我们要找的就是那些 α 不为 0 的,它们就是支撑向量。
∑αiyi = 0
这个结论带来的结果是,我们在推算 α 时,要成对的进行;当我们调高一个 αi 的值时,一定要相应调低另外一个 αj 的值,以满足这个要求。
将该式带回上面拉格朗日公式中。得到结论:
L(w, b, a) = ∑αi - 1/2 ∑αiαjyiyjxixj
此时的拉格朗日函数只包含了一个变量,那就是 α。
现在就是要求 max ∑αi - 1/2 ∑αiαjyiyjxixj
条件是:∑αiyi = 0 且 α >= 0
到目前为止,我们都是假设数据是线性可分的。但实际中往往不这么理想。于是我们引入松弛变量 ξ,且 ξ >= 0 。允许有些数据出现在错误的位置。
这时候,前面的不等式:yi(wTxi + b) -1 >= 0 就变成了:
yi(wTxi + b) -1 + ξ >= 0
要求的最小值从 1/2 * ||w||2 变为:1/2 * ||w||2 = C∑ξ
后面拉格朗日表达式等都要经过一系列的变化。最终发现要求的变成:
max ∑αi - 1/2 ∑αiαjyiyjxixj
条件是:∑αiyi = 0 且 C >= α >= 0
按照坐标上升的思路,我们首先固定除 α1 外的所有参数,然后在 α1 上求极值。但由于要保证 ∑αiyi = 0。所以,在对 α1 进行微量改变的时候,需要对另外一个 α 进行相反的改变。
这里,我们假定取 α1 和 α2 进行优化。根据已有公式得到:
α1y1 + α2y2 + ∑αiyi = 0
其中 ∑ 里,i 取值是从 3 到 n。
于是得到 α1y1 + α2y2 = -∑αiyi
在我们把现在的各个 α 称为 old,调整后的 α 值称为 new,则有:
α1newy1 + α2newy2 = α1oldy1 + α2oldy2 = -∑αiyi
等号右侧的各个 α 都是固定值,于是右侧是个固定的值。我们把它记为 θ:
α1newy1 + α2newy2 = α1oldy1 + α2oldy2 = θ
y1 和 y2 是两个样本点的标签,取值只可能是 1 或 -1。
当它们两者相等时,它们是同号。如果两者都是 1,表达式是:
α1new + α2new = α1old + α2old = θ
因为 α1new 是在 0 - C 之间,所以假设α1new = 0,那么 α2new 可以取到最大值为θ,也就是 α1old + α2old。而 α2new又不能大于 C,所以其最大取值为 min(C, α1old + α2old)。
同理如果 α1new = C,那么 α2new 可以取到最小值为 θ − C,也就是 α1old + α2old − C,而 α2new 最小不能小于0。所以α2new 的下限值就为 max(0, α1old + α2old−C)。
如果 y1 和 y2 相等取 -1 呢?
−α1new − α2new = −α1old − α2old = θ
两边乘以 -1,就是 α1new + α2new = α1old + α2old = -θ,因为不知道−θ是多少,不过一个字母而已,那么用θ代替−θ吧,接下来的讨论过程一模一样。从而属于同类别的时候 α2new 上下限就有了。同理去计算下不同类的时候的上下限。最终的结果是:
if y1 ≠ y2 有 L = max(0, α2old − α1old), H = min(C ,C + α2old − α1old)
if y1 = y2 有 L = max(0, α2old + α1old − C), H = min(C, α2old + α1old)
到这只是给出了 α2new 的范围。
再看一下这个结论:
α1newy1 + α2newy2 = α1oldy1 + α2oldy2 = θ
两边都分别乘以 y1,得到:
α1newy12 + α2newy1y2 = α1oldy12 + α2oldy1y2 = θy1
y12 肯定等于 1,则有:
α1new + α2newy1y2 = α1old + α2oldy1y2 = θy1 = -y1∑αiyi = -∑αiyiy1
∑ 里的取值从 3 开始。
回到原来的问题,我们要求的是
L(w, b, α) = W(α) = ∑αi - 1/2 ∑αiαjyiyjxixj 的最大值。
且有 ∑αiyi = 0, 0 <= αi <= C
经过对偶处理,该问题又可以转换为:
求最小:W(α) = 1/2 ∑∑yiyjK(xi, xj) - ∑αi
我们把 α1 和 α2 分离出来,得到:
W(α) = W(α1) + W(α2) + W(α3…αn)
= 1/2 * K11α12 + 1/2 * K22α22 + y1y2K12α1α2 + y1α1v1 + y2α2v2 - α1 - α2 + W(α3…αn)
其中:
K 表示矩阵的点乘,K22 = x2 * x2, K11 = x1 * x1
v 是一个关于 α1, α2, y1, y2 的表达式:
v = ∑yjαjKij
∑ 里,j 从 3 开始取值
可以看到公式的后面部分和 α1, α2 没关系。又由于有前面的等式:
α1newy1 + α2newy2 = α1oldy1 + α2oldy2
old 是调整之前的值,是已知的。所以,我们可以把 α1 表示为 α2 以及一些已经值的表达式。
α1new = α1old + y1y2(α2old - α2new)
我们要对最后这个值求最小,于是可以求导数再让它等于 0 。就可以算出 α2new:
α2new = α2old - y2(E1 - E2) / η
其中,E表示推测值和实际值的误差。η = 2K(x1, x2) - K(x1, x1) - K(x2, x2)
至此,α1new,α2new 就全部求出来了。然后再通过:
w = ∑αiyixi
可以算出权重值。
对于在边界上的点(支撑向量),它们有:yi(w * x + b) = 1 的等式。然后把bnew对应等式中相同的部分用bold对应的等式里面的东西替换掉,比如说里面有一个求和,拆开后是从α3以后的求和(因为α1,α2要用),这个求和在前后是一样的替换掉。那么一顿替换化简以后对应α1的就会有一个b1new,同理对于α2的就会有一个b2new,他们的最终结果如下:
b1new = bold − E1 − y1(α1new − α1old)K(x1,x1)−y2(α2new−α2old)K(x1, x2)
b2new = bold − E2 − y1(α1new − α1old)K(x1,x1)−y2(α2new−α2old)K(x2, x2)
那么每次更新会出来两个b,选择哪个呢?谁准就选谁,那么怎么判断准不准呢?就是变换后的哪个α在0-C之间,也就是在分界线的边界上,也就是属于支持向量了,那么谁就准。于是就给一个判断:
if 0 ≤ α1new ≤ C, b = b1new
if 0 ≤ α2new ≤ C, b = b2new
其它情况下: b = (b1new + b2new) / 2
至此,所有的数据都能求出来了。现在总结一下 SMO 的过程:
选择两个α,看是否需要更新(如果不满足KKT条件),不需要再选,需要就更新。一直到程序循环很多次了都没有选择到两个不满足KKT条件的点,也就是所有的点都满足KKT了,那么就大功告成了。 从计算上来看,过程大致是:
1.初始化 α 为一个内容全为 0 的矩阵;初始化 b = 0。选取一对样本 x1 和 x2,根据 f(x) = wx + b 以及 w = ∑αyx,得到各自的预测值 y1 和 y2,然后可以算出和真实值之间误差 E1 和 E2。并将 α1 和 α2 做为 α1-old 及 α2-old 保留备用。
2.取其中一个 α1,得到它的取值范围 L 和 H,并裁剪到 [0, C] 之间。如果 L 和 H 的值相等,选取另外两个样本重复前面的步骤。
3.计算 η = 2 * K(x1, x2) - K(x1, x1) - K(x2, x2)
4.根据 η 的值计算 α1-new = α2old - y2(E1 - E2) / η。并将 α1-new 也裁剪到 [0, C] 之间。
5.由于 α1-new 相对 α1-old变了,由于要满足 ∑αy = 0,所以要对 α2-old 也进行一定调整,调整后的值是 α2-new, 它调整的值和 α1-new 相对 α1-old 的量相等,但方向相反。
6.根据公式
b1new = bold − E1 − y1(α1new − α1old)K(x1,x1)−y2(α2new−α2old)K(x1, x2)
b2new = bold − E2 − y1(α1new − α1old)K(x1,x1)−y2(α2new−α2old)K(x2, x2) 算出 b1 和 b2 的值。
再根据当前 α1new 和 α2new 的值判断哪个值对应的 b 更合理。
7.至此,w, b 的值在上述步骤中都调整过一次。现在要做的就是重复 N 次,并且每次选取不同的样本进行计算,以保证参数的泛化能力。
最终当对所有的样本,参数都没法再调整时,这时的参数就是最优参数。当有新的数据过来时,我们把它代入到新参数的公式中,计算得到的值就应该是它的真实值。
案例:简单 smo 算法实现
# -*- coding: utf-8 -*- from numpy import * from time import sleep def loadDataSet(fileName): dataMat = []; labelMat = [] fr = open(fileName) for line in fr.readlines(): lineArr = line.strip().split('\t') dataMat.append([float(lineArr[0]), float(lineArr[1])]) labelMat.append(float(lineArr[2])) return dataMat,labelMat def selectJrand(i,m): j=i #we want to select any J not equal to i while (j==i): j = int(random.uniform(0, m)) return j def clipAlpha(aj,H,L): if aj > H: aj = H if L > aj: aj = L return aj # 数据集、类别标签、常数C(松驰变量)、容错率、退出前最大循环次数 def smoSimple(dataMatIn, classLabels, C, toler, maxIter): # 列表转化为矩阵. dataMatrix = mat(dataMatIn) # 对标签列表进行了转置,最终它是一个列向量 labelMat = mat(classLabels).transpose() # 设置一个默认的常量,在后面的优化中不断变化 b = 0 # 数据集的大小 m 是行数;n是列数 m, n = shape(dataMatrix) # 构建一个空的向量.行数和数据集一样,只有一列 # 它是函数的系数.通过对该系数进行微调,找到最合适的值 alphas = mat(zeros((m, 1))) iter = 0 # 开始循环.循环的最大次数是我们自己定义的 while (iter < maxIter): # 表示当前的 alpha 值是否已经优化过 alphaPairsChanged = 0 # 对每个训练数据集,都进行遍历 for i in range(m): # 分类函数是 f(x) = wx + b # 而 w = ∑αyx, 所以 f(x) = (∑αyx)*x + b = ∑αy<xi, xj> + b, xj 是样本,xi 是待预测的数据 # 第 i 个样本的预测值 fXi = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b # 计算得的值和实际值之差就是当前参数下的误差值 Ei = fXi - float(labelMat[i]) # 如果误差太大,就需要对参数进行优化 # 如果 alphas 的值等于了 0 或 C,表明值在边界上,它不能再优化了。就直接退出 if ((labelMat[i] * Ei < - toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler) and (alphas[i] > 0)): # 从所有的测试样本中随机取一个 j = selectJrand(i, m) # 根据公式计算随机取值的预测值 fXj = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) + b # 计算随机样本计算值的误差 Ej = fXj - float(labelMat[j]) # 将两个样本调整前的 α 复制出来.做为 α-old,方便后面计算 α-new alphaIold = alphas[i].copy() alphaJold = alphas[j].copy() # label 的值只可能是 1 或 -1 # 如果 labelMat[i] 和 labelMat[j] 不相等,表示它们不同符号. # 如果两者相等. 则两者可能同为 1 或 -1 # L 是 alpha 能取值的最小范围, H 是最大范围.但我们要让 alpha 尽量往该范围的中心值靠 # if y1 ≠ y2 有 L = max(0, α2old − α1old), H = min(C ,C + α2old − α1old) # if y1 = y2 有 L = max(0, α2old + α1old − C), H = min(C, α2old + α1old) # 随着计算的进行,会对各个 alpha 进行调整.但我们保证它的值是在 0--C 之间 # 当 L 和 H 相等时,表明没办法再调整了 if labelMat[i] != labelMat[j]: L = max(0, alphas[j] - alphas[i]) H = min(C, C + alphas[j] - alphas[i]) else: L = max(0, alphas[j] + alphas[i] - C) H = min(C, alphas[j] + alphas[i]) # print "L: %s , H: %s" % (L, H) if L == H: print "L==H 无法再优化.对下一个数据进行优化" continue # η = 2K(x1, x2) - K(x1, x1) - K(x2, x2) eta = 2.0 * dataMatrix[i, :]*dataMatrix[j, :].T - dataMatrix[i, :]*dataMatrix[i, :].T - dataMatrix[j, :]*dataMatrix[j, :].T if eta >= 0: print "eta>=0" continue # α2new = α2old - y2(E1 - E2) / η alphas[j] -= labelMat[j]*(Ei - Ej)/eta # 保证参数在 0 - C 之间 alphas[j] = clipAlpha(alphas[j], H, L) # 检查变化后的系数和之前的变化量.如果量不够,说明当前的 α 已经没什么好调整 # 取下一对 α 值调整 if (abs(alphas[j] - alphaJold) < 0.00001): print "j 没多少变化量了.直接进行下一个样本的训练" continue # 对 i 进行修改,修改量与 j 相同,但方向相反.以保证 ∑αy = 0 alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j]) # 通过之前得到的各个值.计算常数项. # b1new = bold − E1 − y1(α1new − α1old)K(x1,x1)−y2(α2new−α2old)K(x1, x2) # b2new = bold − E2 − y1(α1new − α1old)K(x1,x1)−y2(α2new−α2old)K(x2, x2) b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T # 根据条件,判断哪个 b 的值才是更合理的 # if 0 ≤ α1new ≤ C, b = b1new # if 0 ≤ α2new ≤ C, b = b2new # 其它情况下: b = (b1new + b2new) / 2 if (0 < alphas[i]) and (C > alphas[i]): b = b1 elif (0 < alphas[j]) and (C > alphas[j]): b = b2 else: b = (b1 + b2)/2.0 # 表示当前参数做过修改 alphaPairsChanged += 1 print "第 %d 次比较. i:%d, 参数调整 %d 次" % (iter, i, alphaPairsChanged) if (alphaPairsChanged == 0): iter += 1 else: iter = 0 print "循环次数: %d" % iter return b, alphas dataArr, labelArr = loadDataSet('testSet.txt') b, alphas = smoSimple(dataArr, labelArr, 0.6, 0.001, 40) print b # 支持向量个数 print shape(alphas[alphas > 0]) # 支持向量 for i in range(100): if alphas[i] > 0.0: print dataArr[i], labelArr[i]优化版SMO
测试数据 testSet.txt 里的数据如下:
3.542485 1.977398 -1 3.018896 2.556416 -1 7.551510 -1.580030 1 2.114999 -0.004466 -1 8.127113 1.274372 1 7.108772 -0.986906 1总共有 100 条数据。上面的代码运行需要 4 秒左右。如果有 100 万条数据呢,这个效率肯定是不能接受的。回头看上面的逻辑,数学计算方面是无法改变的。但我们选择两个点的方式是可以改变的。目前是采用遍历测试样本做为外循环,然后在内部随机选择一个其它的样本做为内循环,这样会有许多重复的计算。当 alpha 是 0 或 C 时,表明它在边界上,无法再优化。我们其实可以把这一部分点跳过,不参与计算。这样,我们就需要有一个列表来记录各个 alpha 的值并且在计算时跳过边界值。过程是:
选择第一个 alpha,并计算得到 Ei,然后算法通过内循环选择第二个;选择的方法是:先计算各个计算值和真实值的误差 Ej,当 Ei - Ej 的值最大值,选择当前这两个值进行优化。
代码如下:
# -*- coding: utf-8 -*- from numpy import * from time import sleep def loadDataSet(fileName): dataMat = []; labelMat = [] fr = open(fileName) for line in fr.readlines(): lineArr = line.strip().split('\t') dataMat.append([float(lineArr[0]), float(lineArr[1])]) labelMat.append(float(lineArr[2])) return dataMat, labelMat # smo 运算中的一些数据,统一存放在该类中 class optStructK: def __init__(self, dataMatIn, classLabels, C, toler): # 数据矩阵 self.X = dataMatIn # 结果矩阵 self.labelMat = classLabels # 常量 self.C = C self.tol = toler # 样本集长度 self.m = shape(dataMatIn)[0] # 初始化一个变量数据集.和样本一样的行数,只有一列.默认用 0 填充 self.alphas = mat(zeros((self.m, 1))) # y = wt + b 中的常量 b self.b = 0 # 初始化一个缓存集.用来存储各个样本集的误差.尺寸是 m * 2 # 行数和样本一样, 是 m。第一列是表示当前数据是否有效;第二列是实际的误差值.默认都用 0 填充 self.eCache = mat(zeros((self.m, 2))) # 计算各样本在某参数下的误差值 # 计算函数值 wt + b,用它和真实的值相减,得到的值就是误差 def calcEkK(oS, k): fXk = float(multiply(oS.alphas, oS.labelMat).T * (oS.X * oS.X[k, :].T)) + oS.b Ek = fXk - float(oS.labelMat[k]) return Ek # 随机找另一个样本以配对优化 def selectJrand(i, m): # 随机找一个和当前值不同的值 j = i while (j == i): j = int(random.uniform(0, m)) return j # 修剪数据,保证它在取值范围内 def clipAlpha(aj, H, L): if aj > H: aj = H if L > aj: aj = L return aj # 选择另一样本配对优化的第二种方法 def selectJK(i, oS, Ei): maxK = -1; maxDeltaE = 0; Ej = 0 # 将当前样本的误差值设置为 1 和误差中的较大值. oS.eCache[i] = [1, Ei] # 选择缓存数据里,第一列不为空的集合.这些数据就是有效数据 # 初始状态时列表为空 validEcacheList = nonzero(oS.eCache[:, 0].A)[0] if (len(validEcacheList)) > 1: # 遍历缓存的数据.找一个误差最大的 for k in validEcacheList: # 不要和自己比较 if k == i: continue Ek = calcEkK(oS, k) deltaE = abs(Ei - Ek) if (deltaE > maxDeltaE): maxK = k; maxDeltaE = deltaE; Ej = Ek return maxK, Ej else: # 初始状态时,没有符合要求的样本,先用随机选择法选取样本 j = selectJrand(i, oS.m) Ej = calcEkK(oS, j) return j, Ej # 更新缓存数据集中的值.表明当前值已经优化过,且把优化后的误差值记入 # 后面它还可能被选中 def updateEkK(oS, k): Ek = calcEkK(oS, k) oS.eCache[k] = [1, Ek] # 选择一对样本进行优化,并返回是否优化了 def innerLK(i, oS): # 当前选择的参数的误差值 Ei = calcEkK(oS, i) # 如果当前样本已经不可优化,直接返回 if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)): # 选择另一个样本,初始时是随机选择的,后面会从样本中选择误差值最大的值 j, Ej = selectJK(i, oS, Ei) # 将两个样本调整前的 α 复制出来.做为 α-old,方便后面计算 α-new alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy(); # label 的值只可能是 1 或 -1 # 如果 labelMat[i] 和 labelMat[j] 不相等,表示它们不同符号. # 如果两者相等. 则两者可能同为 1 或 -1 # L 是 alpha 能取值的最小范围, H 是最大范围.但我们要让 alpha 尽量往该范围的中心值靠 # if y1 ≠ y2 有 L = max(0, α2old − α1old), H = min(C ,C + α2old − α1old) # if y1 = y2 有 L = max(0, α2old + α1old − C), H = min(C, α2old + α1old) # 随着计算的进行,会对各个 alpha 进行调整.但我们保证它的值是在 0--C 之间 # 当 L 和 H 相等时,表明没办法再调整了 if (oS.labelMat[i] != oS.labelMat[j]): L = max(0, oS.alphas[j] - oS.alphas[i]) H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i]) else: L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C) H = min(oS.C, oS.alphas[j] + oS.alphas[i]) if L == H: print "L==H 无法再优化.对下一个数据进行优化" return 0 # η = 2K(x1, x2) - K(x1, x1) - K(x2, x2) eta = 2.0 * oS.X[i, :] * oS.X[j, :].T - oS.X[i, :] * oS.X[i, :].T - oS.X[j, :] * oS.X[j, :].T if eta >= 0: print "eta>=0" return 0 # α2new = α2old - y2(E1 - E2) / η oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta # 保证参数在 0 - C 之间 oS.alphas[j] = clipAlpha(oS.alphas[j], H, L) # 将当前样本相应的值记入缓存 updateEkK(oS, j) if (abs(oS.alphas[j] - alphaJold) < 0.00001): print "j 没多少变化量了.直接进行下一个样本的训练" return 0 # 对 i 进行修改,修改量与 j 相同,但方向相反.以保证 ∑αy = 0 oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j]) # 同理,将 j 相应的值也记入缓存 updateEkK(oS, i) # 通过之前得到的各个值.计算常数项. # b1new = bold − E1 − y1(α1new − α1old)K(x1,x1)−y2(α2new−α2old)K(x1, x2) # b2new = bold − E2 − y1(α1new − α1old)K(x1,x1)−y2(α2new−α2old)K(x2, x2) b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[i, :].T - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[i,:] * oS.X[j,:].T b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[j, :].T - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[j,:] * oS.X[j,:].T # 根据条件,判断哪个 b 的值才是更合理的 # if 0 ≤ α1new ≤ C, b = b1new # if 0 ≤ α2new ≤ C, b = b2new # 其它情况下: b = (b1new + b2new) / 2 if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1 elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2 else: oS.b = (b1 + b2) / 2.0 # 处理完毕.返回 1 return 1 else: # 未处理.返回 0 return 0 def smoPK(dataMatIn, classLabels, C, toler, maxIter): # 初始化信息 oS = optStructK(mat(dataMatIn), mat(classLabels).transpose(), C, toler) iter = 0 # 是否从整个样本中选取参数对.初始时是这样.随着优化的进行,就直接从缓存列表中进行选择 entireSet = True; # 被修改的参数对计数 alphaPairsChanged = 0 # 遍历 N 次.每次都选两个参数进行优化.如果达到设定的处理次数,或者没有参数被改动了,退出处理 # 过程是:先把样本集中各个值都优化一次.后面就对非边界值进行优化,直到没有可优化的点;这时候再把整个样本集挨个优化一次。 # 这样循环着来,直到达到最大优化次数或者没有可优化的数据 while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)): alphaPairsChanged = 0 # 处理整个样本集 if entireSet: for i in range(oS.m): alphaPairsChanged += innerLK(i, oS) print "全量优化, 第 %d 次循环. 当前 i:%d, 修改值个数: %d" % (iter, i, alphaPairsChanged) iter += 1 else: # 非边界值优化 nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] for i in nonBoundIs: alphaPairsChanged += innerLK(i, oS) print "非边界值优化, 第 %d 次循环.当前 i:%d, 修改值个数: %d" % (iter, i, alphaPairsChanged) iter += 1 if entireSet: # 全量优化后转变为边界优化 entireSet = False elif (alphaPairsChanged == 0): # 如果边界优化一遍循环下来一个值都没有被修改,那就再执行一次全量优化 # 如果全量优化下一个值都没被修改,外层的循环就会退出了 entireSet = True print "iteration number: %d" % iter return oS.b, oS.alphas dataArr, labelArr = loadDataSet('testSet.txt') b, alphas = smoPK(dataArr, labelArr, 0.6, 0.001, 40) print b # 支持向量个数 print shape(alphas[alphas > 0]) # 支持向量 for i in range(100): if alphas[i] > 0.0: print dataArr[i], labelArr[i]使用上面的算法后,结果是秒出。 经过算法得到 alpha, b 的值后。我们就可以通过 alpha 得到 w 的值。于是预测值 wt + b 就可以得到了。如:
dataArr, labelArr = loadDataSet('testSet.txt') b, alphas = smoPK(dataArr, labelArr, 0.6, 0.001, 40) X = mat(dataArr); labelMat = mat(labelArr).transpose() m,n = shape(X) w = zeros((n,1)) for i in range(m): w += multiply(alphas[i] * labelMat[i], X[i,:].T) # 预测 dataMat = mat(dataArr) cat_result = dataMat[0] * mat(w) + b print "预测结果: %s" % cat_result如果结果大于 0,它属于 1 类;如果值小于 0,则属于 -1类。
-
K近邻算法
k-近邻算法
存在一个样本数据集合,也称训练数据集。样本集中每个数据都有标签,即知道数据是属于哪个分类。当我们提供一个无标签的数据时,将新数据的每个特征和现有数据集进行比对,然后找出最相似的标签。通常我们选择样本数据集中前 k 个最相似的数据,k 通常不大于 20。在 k 个数据中,找到出现次数最多的分类作为新数据的分类。
比如,有电影的分类。按亲吻、打斗、追车等特征镜头的数量来进行电影类别的划分。爱情片的亲吻数、打斗、追车数和动作电影,和科幻电影等都不大一样。假设我们已经有一系列数据:
电影名 亲吻 打斗 飞车 类别 电影一 2 9 3 动作 电影二 7 1 1 爱情 电影三 1 4 5 科幻 电影四 1 6 5 科幻 如果现在已经有一个电影,亲吻数、打斗数、飞业数分别是:1,3,6 我们就可以用 k 近邻算法去找出他应该属于哪个类别。该算法可以用来对数据进行类别划分。
优点: 精度高,对异常值不敏感。
缺点: 计算复杂度高,需要大量的训练数据,要大量的资源。数据只能为数值型或标称型。
案例:约会网站推荐对象
约会网站上,每个人都有不同的属性。用户登录并使用服务时,系统会根据你以往的反馈推荐一些对象。比如系统之前推荐过A,B,C,而你反馈的是对A很感兴趣,对B一般,对C讨厌。那么,后续系统就会按A的属性给你推荐相似的人。
用户属性有很多,假设有如下:每年旅行公里数、玩游戏所占时间比例、每周吃甜筒公升数。测试数据如:
张三 40920 8.32 0.95 3 李四 14488 7.15 1.67 2 王五 26052 1.44 0.80 1 赵六 75136 13.14 0.42 1 吴七 38344 1.66 0.13 1 最后一列的数值是喜欢指数。如果现在有一个人,前三列的值分别是:28488、10.52、1.30,我们就可以计算,推测出你对该对象的喜欢指数是多少。
目前有许多用户数据,以 csv 格式保存在文本文件中:user_data.txt 格式就是上述表格。 计算代码如下:
test1.py
# -*- coding: utf-8 -*- from numpy import * import operator # 计算两点之间的距离 # inX 是要测试的数据 # dataSet 是测试样本数据 # labels 是标签向量,即测试数据中的结果列 # k 表示要取多少个相似的结果 def classify0(inX, dataSet, labels, k): dataSetSize = dataSet.shape[0] # 要把输入的向量和测试数据进行比较.测试数据是一个 1000 * 3 的矩阵,而输入数据是 1 * 3 # 所以要用 tile 把输入数据进行填充成和测试数据一样长.然后再计算差值 diffMat = tile(inX, (dataSetSize, 1)) - dataSet # 根据欧氏距离公式.两个向量的距离计算公式是: 向量 [xa, ya] 和 [xb, yb] 距离: (xa-xb)^2 + (ya-yb)^2 然后再取平方根 # 距离计算.向量的各值相减后分别计算平方值 sqDiffMat = diffMat ** 2 # 将各平方值相加 sqDistances = sqDiffMat.sum(axis=1) # 取平方根 distances = sqDistances ** 0.5 # 将矩阵比较结果(输入向量和矩阵中其它每个向量计算的距离值)按从小到大排序 sortedDistIndicies = distances.argsort() classCount = {} # 选择最靠前的 k 个结果 for i in range(k): voteIlabel = labels[sortedDistIndicies[i]] classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1 # 对列表进行排序 sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True) return sortedClassCount[0][0] # 将文件中的内容读取到向量中 def file2matrix(filename): fr = open(filename) # 得到文件中数据的行数 numberOfLines = len(fr.readlines()) # 准备矩阵.长度是文件的行数,内容是空,向量长度为 3 returnMat = zeros((numberOfLines, 3)) # 准备返回的标签 classLabelVector = [] fr = open(filename) index = 0 for line in fr.readlines(): line = line.strip() # 将文件中每一行用 \t 分割成列表 listFromLine = line.split('\t') # 取列表每行的前 3 列.把这三列数据读取到矩阵中 returnMat[index, :] = listFromLine[0:3] # 最后一列做为标签 classLabelVector.append(int(listFromLine[-1])) index += 1 return returnMat, classLabelVector # 归一化数值.将任意范围内的数值处理成 0-1 之间的值. # 因为计算两个值之间的距离时,有可能某一个数据特别大(诸如旅行公里数)。那这一项数据对结果的影响就非常大。 # 但在实际中,不应该让这一个属性就左右计算结果。所以要归一处理。 # 可以用公式: new_value = (old_value - min) / (max - min), 用当前值减去最小值,除以取值范围 def autoNorm(dataSet): # 矩阵中,各列的最小值组成新的向量 minVals = dataSet.min(0) # 矩阵中,各列的最大值组成新的向量 maxVals = dataSet.max(0) # 差值.取值范围 ranges = maxVals - minVals # 矩阵总长度 m = dataSet.shape[0] # dataSet 是 1000 * 3 的矩阵, minVals, ranges 都是 1 * 3的。 # 要想进行矩阵的计算,需要把 min 和 ranges 都用它的值填充满,即 tile(min, (m, 1)); tile(ranges, (m, 1)) old_min = dataSet - tile(minVals, (m, 1)) normDataSet = old_min / tile(ranges, (m, 1)) return normDataSet, ranges, minVals # 测试算法准确度 # 从总数据中取一部分出来,通过算法去计算推测的结果.和真实的结果进行比较,看是否准确. # 这里用 1/10 的数据做为测试 def datingClassTest(): # 用来测试的数据比例 hoRatio = 0.10 # 从文件中加载测试数据 datingDataMat, datingLabels = file2matrix('datingTestSet2.txt') # 归一处理 normMat, ranges, minVals = autoNorm(datingDataMat) # 结果集长度 m = normMat.shape[0] # 用于测试的数据长度 numTestVecs = int(m * hoRatio) # 测试结果有错的值 errorCount = 0.0 # 遍历待测试的每一行 for i in range(numTestVecs): # 计算等测试数据与其它数据的距离 classifierResult = classify0(normMat[i, :], normMat[numTestVecs:m, :], datingLabels[numTestVecs:m], 3) print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]) if (classifierResult != datingLabels[i]): errorCount += 1.0 print "算法错误率: %f" % (errorCount * 100 / float(numTestVecs)) print "算法错误次数: %d 次" % errorCount # 推算某个属性的人会是什么样的结果 def classifyPerson(): resultList = ['不喜欢!', '一般!', '感兴趣!'] fmiles = float(raw_input("每年旅行公里数:")) gamecnt = float(raw_input("花在游戏上的时间比例:")) creamCnt = float(raw_input("每周吃甜筒数:")) # 从文件中加载测试数据 datingDataMat, datingLabels = file2matrix('datingTestSet2.txt') # 归一处理 normMat, ranges, minVals = autoNorm(datingDataMat) inArr = array([fmiles, gamecnt, creamCnt]) # 将输入的内容归一化, 然后再进行推算 classifierResult = classify0((inArr-minVals)/ranges, normMat, datingLabels, 3) print "你对这个人的态度可能是:" + resultList[classifierResult - 1] #datingClassTest() classifyPerson()案例:手写识别系统
目前,手头上有许多二进制图像矩阵,如:
00000000000000111110000000000000 00000000000001111111000000000000 00000000000011111111110000000000 00000000001111111111111000000000 00000000001111111111111000000000 00000000001111111111111000000000 00000000001111100111111100000000 00000000001111000001111110000000 00000000001111000000011111000000 00000000111110000000011111000000 00000000111110000000011110000000 00000001111110000000001110000000 00000001111110000000001111000000 00000001111100000000001111000000 00000011111100000000001111000000 00000011111100000000011110000000 00000011111100000000011110000000 00000011111100000000011110000000 00000001111110000000011110000000 00000001111110000000111110000000 00000001111111000001111100000000 00000001111111000001111100000000 00000001111111000001111000000000 00000000111111000001111000000000 00000000011111111111111000000000 00000000001111111111110000000000 00000000001111111111110000000000 00000000000111111111100000000000 00000000000011111111000000000000 00000000000011111110000000000000 00000000000001111100000000000000 00000000000000001000000000000000每张图都采用 32 * 32 的方式来表示一个数字。同一个数字的写法可能不同,比如上面的 0,还有另外的写法:
00000000000111111000000000000000 00000000001111111100000000000000 00000000011111111110000000000000 00000000011111111111000000000000 00000000111111111111100000000000 00000000111111111111100000000000 00000000111111111111100000000000 00000000111110001111110000000000 00000000111110000111111000000000 00000001111110000011111000000000 00000001111110000001111100000000 00000001111110000001111100000000 00000001111110000000111110000000 00000001111110000000011111000000 00000001111110000000011111000000 00000001111000000000001111000000 00000001111000000000001111000000 00000011111000000000001111000000 00000011111000000000011111000000 00000011111000000000011111000000 00000011111000000000011111000000 00000001111000000000111110000000 00000001111000000001111100000000 00000001111100000111111100000000 00000001111100011111111100000000 00000001111111111111111000000000 00000000111111111111100000000000 00000000111111111111100000000000 00000000011111111111100000000000 00000000011111111111000000000000 00000000001111111000000000000000 00000000000010000000000000000000此案例的想法是:通过一定数量的这种图片训练,让程序能自动识别这种二进制图像矩阵中 0 - 9 的数字。因为同为数字,每个数字的写法不一样,它的矩阵肯定不同。但是通过算法,来计算差异,取最相似的。
每个二进制图像矩阵都保存在一个 txt 文件中。文件名如:0_1.txt,0_3.txt。0 表示该文本里的矩阵表示的数字是 0。_1, _2 表示是第几个文件,无实际意义。那么,现在我们就需要许多用来训练的文本,如:0_1.txt – 0_90.txt; 1_1.txt, 1_90.txt。
由于此例中数据都是二进制的,所以不需要对向量中的值进行归一处理。
整体代码如下:
# -*- coding: utf-8 -*- from numpy import * import operator from os import listdir # 计算两点之间的距离 # inX 是要测试的数据 # dataSet 是测试样本数据 # labels 是标签向量,即测试数据中的结果列 # k 表示要取多少个相似的结果 def classify0(inX, dataSet, labels, k): dataSetSize = dataSet.shape[0] # 要把输入的向量和测试数据进行比较.测试数据是一个 1000 * 3 的矩阵,而输入数据是 1 * 3 # 所以要用 tile 把输入数据进行填充成和测试数据一样长.然后再计算差值 diffMat = tile(inX, (dataSetSize, 1)) - dataSet # 根据欧氏距离公式.两个向量的距离计算公式是: 向量 [xa, ya] 和 [xb, yb] 距离: (xa-xb)^2 + (ya-yb)^2 然后再取平方根 # 距离计算.向量的各值相减后分别计算平方值 sqDiffMat = diffMat ** 2 # 将各平方值相加 sqDistances = sqDiffMat.sum(axis=1) # 取平方根 distances = sqDistances ** 0.5 # 将矩阵比较结果(输入向量和矩阵中其它每个向量计算的距离值)按从小到大排序 sortedDistIndicies = distances.argsort() classCount = {} # 选择最靠前的 k 个结果 for i in range(k): voteIlabel = labels[sortedDistIndicies[i]] classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1 # 对列表进行排序 sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True) return sortedClassCount[0][0] # 把图片数据转换成向量 # 该数据是用 32 * 32 的二进制图像矩阵 def img2vector(filename): # 创建一个矩阵,长度为 1,也就是一个向量。向量长度是 1024.正好用来存储 32 * 32 的矩阵值 returnVect = zeros((1, 1024)) fr = open(filename) for i in range(32): lineStr = fr.readline() for j in range(32): returnVect[0, 32 * i + j] = int(lineStr[j]) return returnVect def handwritingClassTest(): hwLabels = [] # 加载训练数据 trainingFileList = listdir('trainingDigits') m = len(trainingFileList) # 创建矩阵,长度是训练数据的条数.每一个向量长度是 1024 trainingMat = zeros((m, 1024)) # 遍历训练数据。把每张图的向量和真实值进行对应。把真实值作为 label(标签) # 文件名的格式是 2_24.txt, 通过 _ 把前面的 2 分割出来.表示这个文件里的内容真实值应该是 2 for i in range(m): fileNameStr = trainingFileList[i] # 去除文件名中的点和后缀名( .txt ) fileStr = fileNameStr.split('.')[0] # 根据文件名的规则,切割出真实值 classNumStr = int(fileStr.split('_')[0]) # 标签数据,后面算法中要用到.和训练数据一并传到计算方法中 hwLabels.append(classNumStr) trainingMat[i, :] = img2vector('trainingDigits/%s' % fileNameStr) # 待测试数据 testFileList = listdir('testDigits') errorCount = 0.0 mTest = len(testFileList) # 遍历待测试的数据。和前面的训练数据进行计算,为每个待测试的数据找到相似的标签 for i in range(mTest): fileNameStr = testFileList[i] fileStr = fileNameStr.split('.')[0] # 测试数据的真实值 classNumStr = int(fileStr.split('_')[0]) # 得到待测试数据的向量 vectorUnderTest = img2vector('testDigits/%s' % fileNameStr) # 算法得到的值 classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3) print "算法得到的值是: %d, 真实值是: %d" % (classifierResult, classNumStr) if (classifierResult != classNumStr): errorCount += 1.0 print "\n错误总数: %d" % errorCount print "\n错误比例: %f" % (errorCount/float(mTest)) handwritingClassTest()
-
KMP 字符串匹配.
KMP算法
举例来说,有一个字符串”BBC ABCDAB ABCDABCDABDE”,我想知道,里面是否包含另一个字符串”ABCDABD”?
1.首先,字符串”BBC ABCDAB ABCDABCDABDE”的第一个字符与搜索词”ABCDABD”的第一个字符,进行比较。

2.因为B与A不匹配,所以搜索词后移一位。

3.因为B与A不匹配,搜索词再往后移。就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止。

4.接着比较字符串和搜索词的下一个字符,还是相同。

5.直到字符串有一个字符,与搜索词对应的字符不相同为止

这时,最自然的反应是,将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把”搜索位置”移到已经比较过的位置,重比一遍。

- 一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是”ABCDAB”。
- KMP算法的想法是,设法利用这个已知信息,不要把”搜索位置”移回已经比较过的位置,继续把它向后移,这样就提高了效率。

怎么做到这一点呢?可以针对搜索词,算出一张《部分匹配表》(Partial Match Table)。这张表是如何产生的,后面再介绍,这里只要会用就可以了。
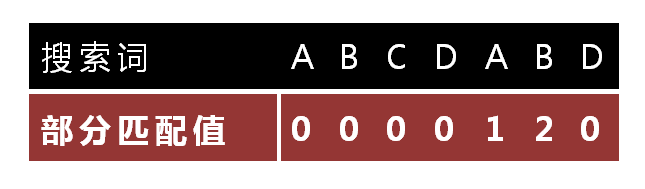
已知空格与D不匹配时,前面六个字符”ABCDAB”是匹配的。查表可知,最后一个匹配字符B对应的”部分匹配值”为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 6 - 2 等于4,所以将搜索词向后移动4位。

因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2(”AB”),对应的”部分匹配值”为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移2位。
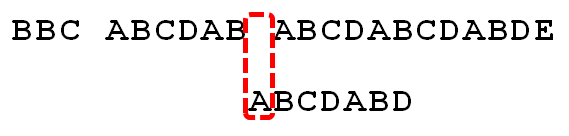
因为空格与A不匹配,继续后移一位。

逐位比较,直到发现C与D不匹配,这时候已经匹配的值是”ABCDAB”,查表得到的匹配值是 2。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位。

逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。
下面介绍《部分匹配表》是如何产生的。
首先,要了解两个概念:”前缀”和”后缀”。 “前缀”指除了最后一个字符以外,一个字符串的全部头部组合;”后缀”指除了第一个字符以外,一个字符串的全部尾部组合。

“部分匹配值”就是”前缀”和”后缀”的最长的共有元素的长度。以”ABCDABD”为例:
“A”的前缀和后缀都为空集,共有元素的长度为0;
“AB”的前缀为[A],后缀为[B],共有元素的长度为0;
“ABC”的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
“ABCD”的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
“ABCDA”的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素 为”A”,长度为1;
“ABCDAB”的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为”AB”,长度为2;
“ABCDABD”的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。
这就是前面看到的表:
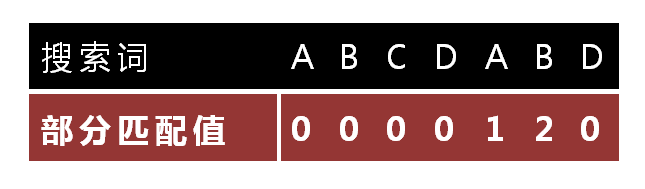
“部分匹配”的实质是,有时候,字符串头部和尾部会有重复。比如,”ABCDAB”之中有两个”AB”,那么它的”部分匹配值”就是2(”AB”的长度)。搜索词移动的时候,第一个”AB”向后移动4位(字符串长度-部分匹配值),就可以来到第二个”AB”的位置。

-
最小二乘法
最小二乘法
又称最小平方法,是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
示例
四个数据点: (1, 6)、(2, 5)、(3, 7)、(4, 10)。我们希望找到一条直线,和这几个点最匹配。即:
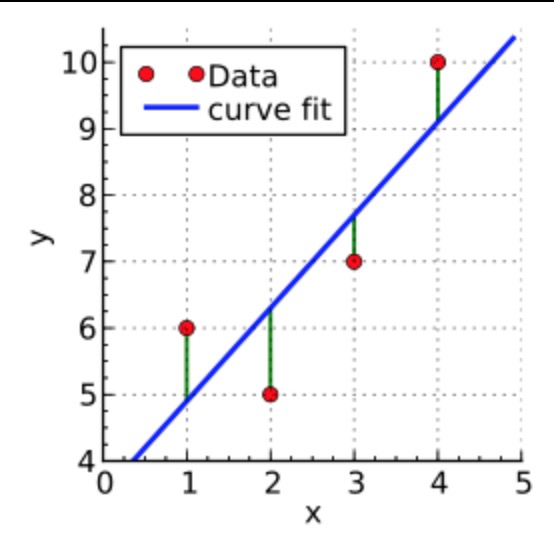
我们假设该直线的表达式是:y = α1 + α2x。那么,按现有数据来看就有:
α1 + 1α2 = 6
α1 + 2α2 = 5
α1 + 3α2 = 7
α1 + 4α2 = 10
该线上点对应的值和真实值是有误差的,我们要做的是找到相应的 α 值,让误差最小。最小二乘法采用的手段是使误差的平方的和最小,即:
S(α1, α2) = [6 - (α1 + 1α2)]2 + [5 - (α1 + 2α2)]2 + [7 - (α1 + 3α2)]2 + [10 - (α1 + 4α2)]2
要求 S 的最小值。而求它最小值又可以通过求 α1, α2的偏导数,并让结果等于 0 得到。即:
∂S/∂α1 = 0 = 8α1 + 20α2 - 56
∂S/∂α2 = 0 = 20α1 + 60α2 - 154
可以解出 α1 = 3.5, α2 = 1.4,也就是说直线的函数是:
y = 3.5 + 1.4x
推导
对由某一变量 t 或多个变量 t1 …… tn 构成的相关变量 y。
-
Redis常见类型的应用场景
Linked List
记录前20个最新登陆的用户Id列表,超出的范围可以从数据库中获得。
//把当前登录人添加到链表里 ret = r.lpush("login:last_login_times", uid) //保持链表只有N位 ret = redis.ltrim("login:last_login_times", 0, N-1) //获得前N个最新登陆的用户Id列表 last_login_list = r.lrange("login:last_login_times", 0, N-1)Sorted Set
以某个条件为权重,比如按顶的次数排序。将你要排序的值设置成 sorted set的score,将具体的数据设置成相应的value,每次只需要执行一条ZADD命令即可。
//将登录次数和用户统一存储在一个sorted set里 zadd login:login_times 5 1 zadd login:login_times 1 2 zadd login:login_times 2 3 //当用户登录时,对该用户的登录次数自增1 ret = r.zincrby("login:login_times", 1, uid) //那么如何获得登录次数最多的用户呢,逆序排列取得排名前N的用户 ret = r.zrevrange("login:login_times", 0, N-1)Set
交集,并集,差集
//book表存储book名称 set book:1:name ”The Ruby Programming Language” set book:2:name ”Ruby on rail” set book:3:name ”Programming Erlang” //tag表使用集合来存储数据,因为集合擅长求交集、并集 sadd tag:ruby 1 sadd tag:ruby 2 sadd tag:web 2 sadd tag:erlang 3 //即属于ruby又属于web的书? inter_list = redis.sinter("tag.web", "tag:ruby") //即属于ruby,但不属于web的书? inter_list = redis.sdiff("tag.ruby", "tag:web") //属于ruby和属于web的书的合集? inter_list = redis.sunion("tag.ruby", "tag:web")bitmaps
Redis支持对String类型的value进行基于二进制位的置位操作。通过将一个用户的id对应value上的一位,通过对活跃用户对应的位进行置位,就能够用一个value记录所有活跃用户的信息。
setbit 2014-07-28-login 1053 1 setbit 2014-07-28-login 89887 1 bitcount 2014-07-28-login (integer) 2通过
setbit将 bitmap 对应的位设置为 1。比如100100的意思是ID为 2, 5 的两个人已登录。bitcount表示们为 1 的有多少个,这样就表示当前登录的用户有多少。
-
Select/poll/epoll
流
首先我们来定义流的概念,一个流可以是文件,socket,pipe等等可以进行I/O操作的内核对象。
不管是文件,还是套接字socket,还是管道,我们都可以把他们看作流。
在 I/O 操作里,通过read,我们可以从流中读入数据;通过write,我们可以往流写入数据。
现在假定一个情形,我们需要从流中读数据,但是流中还没有数据,(典型的例子为:用户访问某WEB页面,和服务器建立了 socket 连接。客户端要从socket读数据,但是服务器还没有把数据传回来),这时候该怎么办?
阻塞
比如某个时候你在等快递,但是你不知道快递什么时候过来,而且你没有别的事可以干(或者说接下来的事要等快递来了才能做);
那么你可以去睡觉了,因为你知道快递把货送来时一定会给你打个电话(假定一定能叫醒你)。
非阻塞忙轮询
你知道快递员的手机号,然后每分钟给他挂个电话:“你到了没?”
很明显一般人不会用第二种做法,自己花费大量的精力,还占用了快递员大量的时间。
第一种方法经济而简单,经济是指消耗很少的CPU时间,如果线程睡眠了,就掉出了系统的调度队列,暂时不会去瓜分CPU宝贵的时间片了。
缓冲区
缓冲区的引入是为了减少频繁I/O操作而引起频繁的系统调用),当操作一个流时,更多的是以缓冲区为单位进行操作。对于内核来说,也需要缓冲区,就是内核缓冲区。
假设有一个管道,进程A为管道的写入方,B为管道的读出方。
假设一开始内核缓冲区是空的,B作为读出方,被阻塞着,在等待数据写入。然后首先A往管道写入,这时候内核缓冲区由空的状态变到非空状态,内核就会产生一个事件告诉B该醒来了,这个事件姑且称之为 “缓冲区非空”。
但是“缓冲区非空”事件通知B后,B却还没有读出数据;且内核许诺了不能把写入管道中的数据丢掉,这个时候,A写入的数据会滞留在内核缓冲区中。
如果内核也缓冲区满了,B仍未开始读数据,最终内核缓冲区会被填满,这个时候会产生一个I/O事件,告诉进程A,你该等等(阻塞)了,我们把这个事件定义为 “缓冲区满”。
假设后来B终于开始读数据了,于是内核的缓冲区空了出来,这时候内核会告诉A,内核缓冲区有空位了,你可以从阻塞中醒来了,继续写数据了,我们把这个事件叫做 “缓冲区非满”。
也许事件已经通知了A,但是A也没有数据写入了,而B继续读出数据,直到内核缓冲区空了。这个时候内核就告诉B,你需要阻塞了!我们把这个事件定为 “缓冲区空”。
这四个情形涵盖了四个I/O事件,缓冲区满,缓冲区空,缓冲区非空,缓冲区非满(注都是说的内核缓冲区,且这四个术语都是捏造的,仅为解释其原理而造)。这四个I/O事件是进行阻塞同步的根本。。
阻塞I/O的缺点
阻塞I/O模式下,一个线程只能处理一个流的I/O事件。如果想要同时处理多个流,要么多进程(fork),要么多线程(pthread_create),很不幸这两种方法效率都不高。
于是再来考虑非阻塞忙轮询的I/O方式,我们发现我们可以同时处理多个流了。
我们只要不停的把所有流从头到尾检查一遍,然后又从头开始。这样就可以处理多个流了,但这样的做法显然不好,因为如果所有的流都没有数据,那么只会白白浪费CPU。
这里要补充一点,阻塞模式下,内核对于I/O事件的处理是阻塞或者唤醒,而非阻塞模式下则把I/O事件交给其他对象(后文介绍的select以及epoll)处理甚至直接忽略。
select/poll
为了避免CPU空转,可以引进了一个代理(一开始有一位叫做 select 的代理,后来又有一位叫做 poll 的代理,不过两者的本质是一样的)。这个代理比较厉害,可以同时观察许多流的I/O事件,在空闲的时候,会把当前线程阻塞掉,当有一个或多个流有I/O事件时,就从阻塞态中醒来,然后就会轮询一遍所有的流。
于是,如果没有I/O事件产生,我们的程序就会阻塞在select处。但是依然有个问题,我们从select那里仅仅知道了,有I/O事件发生了,但却并不知道是那几个流(可能有一个,多个,甚至全部),我们只能无差别轮询所有流,找出能读出数据,或者写入数据的流,对他们进行操作。
使用select,同时处理的流越多,每一次轮询时间就越长。所以在高并发的情况下会很慢。 select 最不能忍受的是一个进程所打开的 TCP连接是有一定限制的,由FD_SETSIZE设置,默认值是1024。对于那些需要支持的上万连接数目的IM服务器来说显然太少了。
虽然可以选择多进程的解决方案(传统的Apache方案),不过虽然linux上面创建进程的代价比较小,但仍旧是不可忽视的,加上进程间数据同步远比不上线程间同步的高效,所以也不是一种完美的方案。
假设我们的服务器需要支持100万的并发连接,则在__FD_SETSIZE 为1024的情况下,则我们至少需要开辟1k个进程才能实现100万的并发连接。
select 是用数组存储监视的流,应用程序需要遍历整个数组才能发现哪些流发生了事件。而 poll使用了链表,对监视文件的数量没有限制,扩展方便,但每次一样要遍历才能发现哪些流有事件。
epoll
epoll可以理解为event poll,不同于忙轮询和无差别轮询,epoll之会把哪个流发生了怎样的I/O事件通知我们。
假如有100万个客户端同时与一个服务器进程保持着TCP连接。而每一时刻,通常只有几百上千个TCP连接是活跃的(事实上大部分场景都是这种情况)。如何实现这样的高并发?
在select/poll时代,服务器进程每次都把这100万个连接告诉操作系统(从用户态复制句柄数据结构到内核态),让操作系统内核去查询这些套接字上是否有事件发生,轮询完后,再将句柄数据复制到用户态,让服务器应用程序轮询处理已发生的网络事件,这一过程资源消耗较大,因此,select/poll一般只能处理几千的并发连接。
epoll的设计和实现与select完全不同。epoll通过在Linux内核中申请一个简易的文件系统。把原先的select/poll调用分成了3个部分:
- 调用epoll_create()建立一个epoll对象(在epoll文件系统中为这个句柄对象分配资源)
- 调用epoll_ctl()。通过此调用向epoll对象中添加、删除、修改感兴趣的事件
- 调用epoll_wait收集发生的事件的连接
这样,只需要在进程启动时建立一个epoll对象,然后在需要的时候向这个epoll对象中添加或者删除连接。当某一进程调用epoll_create方法时,Linux内核会创建一个eventpoll结构体,这个结构体中有两个成员与epoll的使用方式密切相关。如:
struct eventpoll{ .... /*红黑树的根节点,这颗树中存储着所有添加到epoll中的需要监控的事件*/ struct rb_root rbr; /*双链表中则存放着将要通过epoll_wait返回给用户的满足条件的事件*/ struct list_head rdlist; .... };每一个epoll对象都有一个独立的eventpoll结构体,用于存放通过epoll_ctl方法向epoll对象中添加进来的事件。这些事件都会挂载在红黑树中,如此,重复添加的事件就可以通过红黑树而高效的识别出来(红黑树的插入时间效率是lgn,其中n为树的高度)。
所有添加到epoll中的事件都会与设备(网卡)驱动程序建立回调关系,也就是说,当相应的事件发生时会调用这个回调方法。
在 epoll中,对于每一个事件,都会建立一个epitem结构体,如下所示:
struct epitem{ struct rb_node rbn;//红黑树节点 struct list_head rdllink;//双向链表节点 struct epoll_filefd ffd; //事件句柄信息 struct eventpoll *ep; //指向其所属的eventpoll对象 struct epoll_event event; //期待发生的事件类型 }当调用epoll_wait检查是否有事件发生时,只需要检查eventpoll对象中的rdlist双链表中是否有epitem元素即可。如果rdlist不为空,则把发生的事件复制到用户态,同时将事件数量返回给用户。
epoll 数据的结构图示如下:
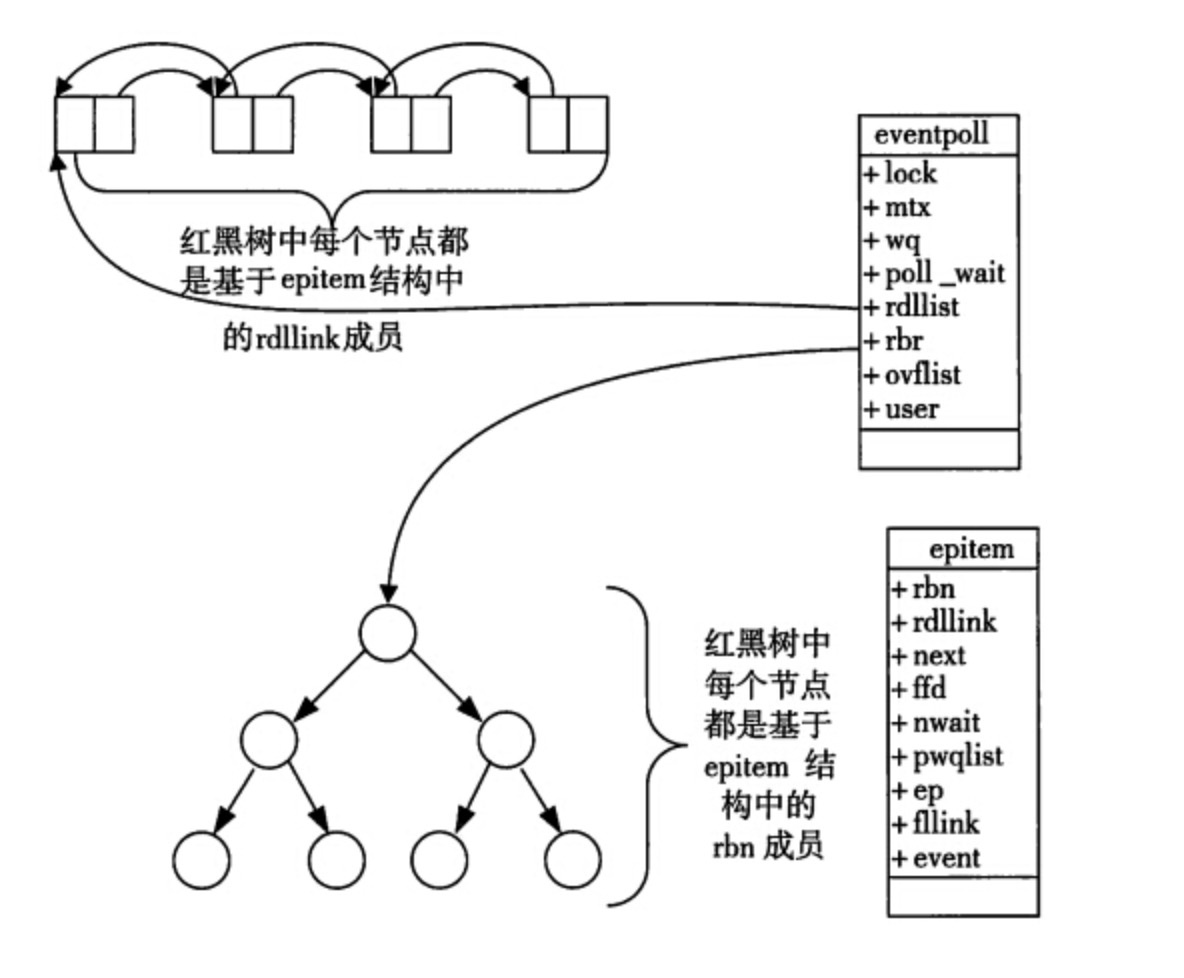
通过红黑树和双链表数据结构,并结合回调机制,造就了epoll的高效。
而且 epoll 没有 FD_SETSIZE 限制,它所支持的TCP连接数上限是最大可以打开文件的数目,这个数字一般远大于2048,举个例子,在1GB内存的机器上大约是10万左右,具体数目可以cat /proc/sys/fs/file-max 查看.
在较小的并发中。select 方式在内存使用和即时效率上会稍优于 epoll, 但在现在硬件如此优越的情况下,这种差异可以不考虑到实际中,我们更关心在高并发时的情况。
epool 的处理方式会更节省CPU使用率。当然,也会更省内存。
传统的 Apache 服务器就是使用的 select 模型,Nginx 上可以配置成使用 epoll。
-
CGI 和 FastCGI php-fpm
CGI
CGI (Common Gateway Interface) 通用网关接口。
CGI 是WWW技术中最重要的技术之一,有着不可替代的重要地位。CGI是外部应用程序(CGI程序)与Web服务器之间的接口标准,是在CGI程序和Web服务器之间传递信息的规程。CGI规范允许Web服务器执行外部程序,并将它们的输出发送给Web浏览器。
CGI可以用任何一种语言编写,只要这种语言具有标准输入、输出和环境变量。
最好选用易于归档和能有效表示大量数据结构的语言,例如UNIX环境中:
Perl (Practical Extraction and Report Language)
Bourne Shell或者Tcl (Tool Command Language)
PHP
CGI 程序工作原理
web server(如: Nginx)只是内容的分发者。比如,如果请求/index.html,那么web server会去文件系统中找到这个文件,发送给浏览器,这里分发的是静态资源。
如果现在请求的是/index.php,根据配置文件,Nginx知道这个不是静态文件,需要去找PHP解析器来处理,那么他会把这个请求简单处理后交给PHP解析器。
此时CGI便是规定了要传什么数据,以什么格式传输给php解析器的协议。
当 web server收到 /index.php这个请求后,会启动对应的CGI程序,这里就是PHP的解析器。接下来PHP解析器会解析php.ini文件,初始化执行环境,然后处理请求,再以CGI规定的格式返回处理后的结果,退出进程。web server再把结果返回给浏览器。
CGI针对每个http请求都是fork一个新进程来进行处理,每一个Web请求PHP都必须重新解析php.ini、重新载入全部扩展并重初始化全部数据结构。然后这个进程会把处理完的数据返回给web服务器,最后web服务器把内容发送给用户,刚才fork的进程也随之退出。 如果下次用户还请求动态资源,那么web服务器又再次fork一个新进程,周而复始的进行。
从这个过程就可以看出有许多重复的步骤,浪费了许多时间和资源。这就是 FastCGI改进的地方。
FastCGI 工作原理
Fastcgi则会先fork一个master,解析配置文件,初始化执行环境,然后再fork多个worker。
当请求过来时,master会传递给一个worker,然后立即可以接受下一个请求。这样就避免了重复的劳动,效率自然是高。而且当worker不够用时,master可以根据配置预先启动几个worker等着;当空闲worker太多时,也会停掉一些,这样就提高了性能,也节约了资源。
FastCGI生命周期可能如下:
- Web Server启动时载入FastCGI进程管理器(IIS ISAPI, Apache Module, php-fpm)
- FastCGI进程管理器自身初始化,启动多个CGI解释器进程(可见多个php-cgi)并等待来自Web Server的连接。
- 当客户端请求到达Web Server时,FastCGI进程管理器选择并连接到一个CGI解释器。Web server将CGI环境变量和标准输入发送到FastCGI子进程php-cgi。
- FastCGI子进程完成处理后将标准输出和错误信息从同一连接返回Web Server。当FastCGI子进程关闭连接时,请求便告处理完成。
- FastCGI子进程接着等待并处理来自FastCGI进程管理器(运行在Web Server中)的下一个连接。 在CGI模式中,php-cgi在此便退出了。
FastCGI像是一个常驻(long-live)型的CGI,它可以一直执行着,只要激活后,不会每次都要花费时间去fork一次(这是CGI最为人诟病的fork-and-execute 模式)。
FastCGI是语言无关的、可伸缩架构的CGI开放扩展,其主要行为是将CGI解释器进程保持在内存中并因此获得较高的性能。CGI解释器的反复加载是CGI性能低下的主要原因,如果CGI解释器保持在内存中并接受FastCGI进程管理器调度,则可以提供良好的性能、伸缩性等等。
大多数Fastcgi实现都会维护一个进程池。php-fpm 就是这样一种方式。另外, swoole 也可以替代 php-fpm 来实现这一功能。
-
BloomFilter
Bloom Filter是由Bloom在1970年提出的一种多哈希函数映射的快速查找算法。通常应用在一些需要快速判断某个元素是否属于集合,但是并不严格要求100%正确的场合。
场景
假设要你写一个网络蜘蛛(web crawler)。由于网络间的链接错综复杂,蜘蛛在网络间爬行很可能会形成“环”。为了避免形成“环”,就需要知道蜘蛛已经访问过那些URL。给一个URL,怎样知道蜘蛛是否已经访问过呢?稍微想想,就会有如下几种方案:
- 将访问过的URL保存到数据库。
- 用HashSet将访问过的URL保存起来。那只需接近O(1)的代价就可以查到一个URL是否被访问过了。
- URL经过MD5或SHA-1等单向哈希后再保存到HashSet或数据库。
- Bit-Map方法。建立一个BitSet,将每个URL经过一个哈希函数映射到某一位。
方法1~3都是将访问过的URL完整保存,方法4则只标记URL的一个映射位。
以上方法在数据量较小的情况下都能完美解决问题,但是当数据量变得非常庞大时问题就来了。
方法1的缺点
数据量变得非常庞大后关系型数据库查询的效率会变得很低。而且每来一个URL就启动一次数据库查询,代价略大。
方法2的缺点
太消耗内存。随着URL的增多,占用的内存会越来越多。就算只有1亿个URL,每个URL只算50个字符,就需要5GB内存。
方法3的缺点
由于字符串经过MD5处理后的信息摘要长度只有128Bit,SHA-1处理后也只有160Bit,因此方法3比方法2节省了好几倍的内存。
方法4的缺点
消耗内存是相对较少的,但缺点是单一哈希函数发生冲突的概率太高。Hash表冲突的时候会把冲突的键里建一个链表,将多个值放到链表里,但链表的随机访问很慢。若要降低冲突发生的概率到1%,就要将BitSet的长度设置为URL个数的100倍。
实质上上面的算法都忽略了一个重要的隐含条件:允许小概率的出错,不一定要100%准确!也就是说少量url实际上没有没网络蜘蛛访问,而将它们错判为已访问的代价是很小的——大不了少抓几个网页。
Bloom Filter的算法
上面方法4的思想已经很接近Bloom Filter了。方法四的致命缺点是冲突概率高,为了降低冲突的概念,Bloom Filter使用了多个哈希函数,而不是一个。
Bloom Filter算法如下
创建一个 m 位BitSet,先将所有位初始化为0,然后选择k个不同的哈希函数。第i个哈希函数对字符串str 哈希的结果记为h(i,str),且h(i,str)的范围是 0 到 m-1。
记录字符串过程
下面是每个字符串处理的过程,首先是将字符串str“记录”到BitSet中的过程:
对于字符串str,分别计算 h(1,str),h(2,str)…… h(k,str)。然后将BitSet的第 h(1,str)、h(2,str)…… h(k,str)位设为1。
这样就将字符串str映射到BitSet中的k个二进制位了。
检查字符串是否存在的过程
下面是检查字符串str是否被BitSet记录过的过程:
对于字符串str,分别计算 h(1,str),h(2,str)…… h(k,str)。然后检查 BitSet的第 h(1,str)、h(2,str)…… h(k,str)位是否为1,若其中任何一位不为1则可以判定 str一定没有被记录过。若全部位都是1,则“认为”字符串str存在(也有可能不存在,因为其它字符串计算出来的值在某个位置上可能和当前字符串有交叉)。
删除字符串过程
字符串加入了就被不能删除了,因为删除会影响到其他字符串。
Bloom Filter跟单哈希函数Bit-Map不同之处在于:Bloom Filter使用了k个哈希函数,每个字符串跟k个bit对应。从而降低了冲突的概率。